(Feladat azonosítója: VF_000025 )
Témakör: *Geometria (szerkesztés)
Szerkesszünk derékszögű háromszöget, ha adott az átfogó $c$ és tudjuk azt, hogy az átfogóhoz tartozó súlyvonal mértani középarányos a két befogó között.
Nem megy az általánosság rovására, ha egyszer és mindenkorra feltételezzük, hogy $a>b$. Pitagorasz tétele szerint
feltételünk szerint (mivel a súlyvonal $\frac{c}{2})$
és -t összeadva, ill. kivonva nyerjük
amiből
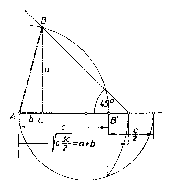
A szerkesztés ezek alapján többféleképpen is történhet. $\alpha )$ és összeadásából nyerjük, hogy $a=\frac{c\sqrt 6 +c\sqrt 2 }{4}$, amely szakasz könnyen szerkeszthető ($c\sqrt 6 $ mértani középarányos 2$c$ és 3$c$ között, $c\sqrt 2 $ pedig $c$ és 2$c$ között). $a$ és $c$ birtokában a keresettháromszög szerkesztése triviális. $\beta )$ alapján $a+b$, mint mértani középarányos $c$ és $\frac{3}{2}c$ között megszerkeszthető. Az $a+b$ és $c$ szakaszok birtokában a háromszög szerkesztése a tankönyvből ismeretes (1. ábra). $\gamma )$ szerint $a-b$ olyan négyzet átlója, melynek oldala $\frac{c}{2}$. $a-b$ és $c$ birtokában a derékszögű háromszög ismert módon (2. ábra) megszerkeszthető. Mindhárom esetben könnyen kimutatható, hogy az így megszerkesztett háromszög tényleg eleget tesz követelményünknek. Pl. az utóbbi esetben Pitagorasz-tétele alapján
amiből
és így tényleg $ab=\frac{c^2}{4}.$
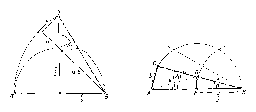
Oldalak helyett szögeket is kiszámíthatunk, mint azt az alábbi 2-4. megoldások mutatják.
2. Megoldás
Képzeljük a feladatot megoldottnak. A betűzést a 3. ábra mutatja. Jelöljük az AB átfogó felező pontját $F$-fel, tehát $FA=FB=\frac{c}{2}$. Az $F$-ben az átfogóra emelt merőleges messe a $BC=a$ befogót $D$-ben. Legyen $AD=DB=x$. A szögek egyenlősége miatt
és így
amiből
De a feltétel szerint
és így$x=2b$. Az ACD derékszögű háromszögben $\sin CDA\angle =\sin 2\beta =\frac{b}{x}=\frac{b}{2b}=\frac{1}{2}$, amiből$ 2\beta =30^{\circ}$, vagyis $\beta =15^{\circ}$, mely szög könnyen szerkeszthető.
3. Megoldás
A jelöléseket megtartva
A feltétel szerint
vagyis, $\frac{2}{c^2}$-tel szorozva
azaz
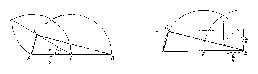
ahonnan $\left( {0<2\alpha <180^{\circ}} \right)$ $ 2\alpha =30^{\circ}$ ill. $ 150^{\circ}$, $a>b$ miatt$\alpha =75^{\circ}$.
4. Megoldás
Az előbbi jelöléseket megtartva jelöljük az AFC$\angle $-et $\varphi $-vel (4. ábra). Az $AFC\Delta $ területe a fele az $ABC\Delta $ területének. Tehát
vagyis $c^2\sin \varphi =2ab$, amiből $\sin \varphi =\frac{2ab}{c^2}$. De a feltétel szerint $ab=\frac{c^2}{4}$, vagyis $ 2ab=\frac{c^2}{2}$, és így $\sin \varphi =\frac{1}{2}$, vagyis $\varphi =30^{\circ}$. A $C$ pont megszerkesztése a körülírt körön egyszerűbb már nem lehet.
5. Megoldás
A legegyszerűbb megoldáshoz (ha nem is a legegyszerűbb szerkesztéshez) jutunk, ha feltételünket ,,helyesen'' olvassuk. Feltételünk szerint
ab a háromszög kétszeres területe, tehát $c\cdot \frac{c}{4}$ is az , vagyis $\frac{c}{4}$ a háromszögnek az átfogóhoz tartozó magassága. A szerkesztést az 5. ábra mutatja. Az utóbbi megoldásnál közvetlenül nyilvánvaló,hogy a megszerkesztett háromszög teljesíti a feladatban kirótt felételt: $ab=c\cdot \frac{c}{4}=\frac{c^2}{4}$. A 2-4. megoldásnál (ahol tulajdonképpen kiszámítottuk, hogy $\alpha =75^{\circ}$ és $\beta =150^{\circ})$ a közvetkezőképpen igazolhatjuk szerkesztésünk helyességét:
és így
De anélkül, hogy a háromszög oldalait vagy szögeit kiszámítanánk, is megoldhatjuk feladatunkat, amint azt az alábbi 6-7. megoldások mutatják.
6. Megoldás
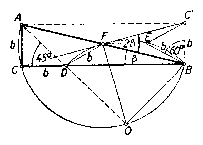
Képzeljük a feladatot megoldottnak. A betűzést a 6. ábra mutatja. Szerkesszük meg azt a kört, amely a CF egyenest $F$-ben érinti és a $B$ csúcsponton is átmegy. Legyen ennek a körnek középpontja $O$ és messe ez a kör a BC befogót másodszor $D$-ben. Mivel $CF^2=CB\cdot CD$, vagyis $\left( {\frac{c}{2}} \right)^2=a\cdot CD$ azért a feladat szerint $CD=b.$ Ha kimutatjuk hogy $O$ rajta van az AO egyenesen, akkor lényegében a 2. megoldásban nyert szerkesztéshez jutottunk, de más indokolással. Mivel BFC egyenlőszárú háromszögből$FCD\angle =FBD\angle =\beta $, másrészt $CFD\angle =\beta $, mint az FD ív fölötti húr-érintőszög, azért CDF egyenlő szárú háromszög és$FD=Cd=b.$ Az FB ívhez tartozó húr-érintő szög, mint a $BFC\Delta $ külső szög $ 2\beta $, tehát ez az ív kétszerese az FD ívnek. Az $E$ felezőpontját berajzolva, a húrokra $FE=EB=b$ és $FE\left\| {DB} \right.$. Az $ABC\Delta $-et téglalappá egészítve ki FE ennek a középvonalán fekszik. Így $CE'=EB=b$, másrészt $BC'=AC=b$, tehát a $BEC'$ szabályos háromszögből $C'BE\angle =60^{\circ}$, s így
Ugyanekkorák az FB íven nyugvó kerületi szögek, és így a középponti szög $BOF\angle =60^{\circ}$ és $BO=FO=BF=\frac{c}{2}$ a kör sugara. A BOD egyenlőszárú háromszög alapján nyugvó szög
Ebből következik,hogy ez a háromszög derékszögű, továbbá $A$, $D$ és $O$ egy egyenesbe esnek és $O$ (a $C$-vel együtt) az AB fölötti félkörön van. Eszerint a szerkesztés menete: az $AB=c$ átmérő fölötti félkört a $BO=\frac{c}{2}$ távolsággal elmetszve, majd az AO egyenest az $OD=\frac{c}{2}$ távolsággal elmetszve, a BD egyenes metszi ki az AB fölötti félkörből a keresett háromszög $C$ csúcsát. A szerkesztés igazolása: Mivel az $ABO\Delta $ szögei $ 30^{\circ}$, $ 60^{\circ}$ és $ 90^{\circ}$, azért az $O$ körüli $\frac{c}{2}$ sugarú körnek az AB-vel való $F$ metszéspontjára $FOB\Delta $ szabályos, mert $FBO\angle =60^{\circ}$, tehát $F$ felezőpont, $CF=\frac{c}{2}$, mint a derékszögű háromszög súlyvonala, továbbá $BFO\angle =60^{\circ}$. BOD egyenlőszárú derékszögű háromszög, tehát $ADC\angle =DAC\angle =45^{\circ}$, $CD=CA=b$; másrészt az AFC egyenlőszárú háromszögben $CAF\angle =45^{\circ}+30^{\circ}=75^{\circ}$, s így az $AFC\angle =30^{\circ}$. Ebből következik, hogy
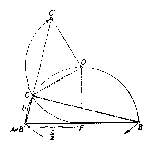
Így CF érinti az $O$ középpontú kört, s így
tehát az $ABC\Delta $ megfelel a kívánalmaknak.
7. Megoldás
Az adott $AB=c$ átfogó fölé rajzolt $F$ középpontú Thales-körben az AB átmérőre merőleges sugár végpontját jelöljük $O$-val (7. ábra). $O$ körül $OF=\frac{c}{2}$ sugárral rajzolt kör metszi ki a Thales-körből a keresett $C$ pontot. (Ez tulajdonképpen az 5. megoldásban nyert szerkesztés, ismét más megindokolással.) Forgassuk el a $BC=a$ befogót $O$ körül $ 90^{\circ}$-kal az óra járásával megegyező irányban, akkor a $B$ elforgatása a $B'$ az $A $ pontba kerül, $C$ elforgatása pedig $C'$, és $B'C'\equiv AC'\bot BC$. Mivel AC is merőleges BC-re, azért a $C'$ pont az AC befogó meghosszabbításán fekszik. A szerkesztés szerint az $AF=\frac{c}{2}$ az $O$ körül rajzolt körnek az $A$ pontból húzott érintője, és így