Az $ ABCD $ négyzet oldalai 4 méter hosszúak. A négyzetbe az ábrán látható módon az $ EFGH $ paralelogrammát írjuk.
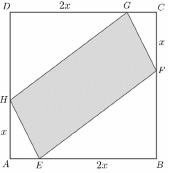
Az $ AH $ és a $ CF $ szakasz hossza $ x $ méter, a $ BE $ és a $ DG $ szakasz hossza $ 2x $ méter $ (0 < x < 2) $.
a) Igazolja, hogy a beírt paralelogramma területe ($ m^2 $-ben mérve): $ T(x) = 4 x^2 -12 x + 16 $.
b) Határozza meg az $ x $ értékét úgy, hogy a beírt paralelogramma területe a lehető legkisebb legyen!
c) Számítsa ki a beírt paralelogramma szögeit, ha $ x = 1,25 $.
a) Egy mértani sorozat negyedik tagja 12, a kilencedik tagja 384. Számítsa ki a sorozat első hat tagjának az átlagát, és az átlagtól mért átlagos abszolút eltérését!
b) Hány olyan pozitív egész szám van, amelyben a számjegyek szorzata és összege is 12?
Oldja meg az alábbi egyenleteket a valós számok halmazán!
a) $\left(\dfrac{1}{3} \right)^{2x+1}+ \left(\dfrac{1}{9} \right)^{x+1}=324$
b) $\sqrt{6x-24 }=\sqrt{2x-7 } -1$
Egy bűvész két egyforma „dobótetraédert” használ az egyik mutatványához. A dobótetraéder alakja olyan szabályos háromoldalú gúla, amelynek alapéle 6 cm hosszú, az oldalélei pedig $ 30^\circ $-os szöget zárnak be az alaplap síkjával.
a) Határozza meg a tetraéder térfogatát!
A tetraéderrel 1-est, 2-est, 3-ast vagy 4-est lehet dobni (a dobás eredményének az alsó lapon lévő számot tekintjük). Az 1-es, a 2-es, illetve a 3-as dobásának valószínűsége egyenlő. A 4-es dobásának valószínűsége ötször akkora, mint az 1-es dobásé.
b)Ha a bűvész a két dobótetraédert egyszerre dobja fel, akkor mennyi annak a valószínűsége, hogy a dobott számok összege 6 lesz?


