Látogatók
Összes: 6 045 740 Mai: 4 535
|
1. találat: Matematika emelt szintű érettségi, 2019. október, II. rész, 5. feladat
Témakör: *Geometria (Azonosító: mme_201910_2r05f )
a) Döntse el, hogy igaz-e a következő állítás! Válaszát indokolja! Ha egy háromszög két magassága egyenlő hosszúságú, akkor a háromszög egyenlő szárú. Egy háromszögben a szokásos jelölésekkel $a = 3$, $b = \sqrt{ 27 }$ és $\beta = 2\alpha$. b) Számítsa ki a háromszög szögeit! Az egységnyi oldalú, szabályos $ABC$ háromszögbe olyan $PQRS$ téglalapot írunk, melynek $PQ$ oldala az $AB$ oldalra illeszkedik, $R$ a $BC$ oldal pontja, $S$ pedig a $CA$ oldalé. c) Határozza meg a $PQRS$ téglalap területének maximális értékét!
*Kombinatorika (Azonosító: mme_201910_2r06f )
Legyen az $U$ alaphalmaz a legalább 4 pontú egyszerű gráfok halmaza. Az $F$ halmaz az $U$ elemei közül pontosan azokat tartalmazza, amelyek fagráfok, a $G$ halmaz pontosan azokat, amelyek összefüggő gráfok, a $H$ halmaz pedig pontosan azokat, amelyek 6 pontú gráfok. a) Az alábbi ábrán satírozással jelölje meg, és halmazműveletekkel is adja meg az $U$-nak azt a részhalmazát, amelyik üres halmaz! b) A megadott Venn-diagram minden egyes további részébe rajzoljon pontosan egy lehetséges gráfot! 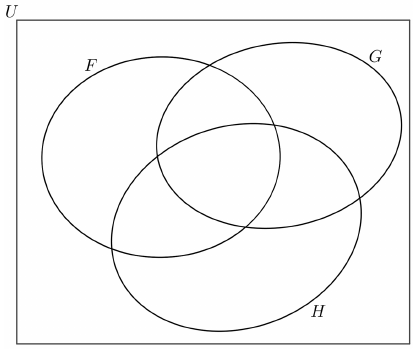
Egy telephely $K$, $L$, $M$, $N$, $O$, $P$, $Q épületei közül az éjszakai első ellenőrzés során ötöt ellenőriz a biztonsági őr. c) Hányféleképpen tervezheti meg az útvonalát, ha a $K$ és $L$ épületeket mindenképpen ellenőrzi? (Két útvonal különböző, ha a két út során más épületeket, vagy ugyanazokat az épületeket, de más sorrendben ellenőriz a biztonsági őr.) Megrajzoltuk az $ABCDE$ konvex ötszög oldalait és átlóit, majd a megrajzolt szakaszok mindegyikét vagy kékre, vagy zöldre színeztük. A színezés befejezése után észrevettük, hogy nincs olyan háromszög, amelynek csúcsai az $A$, $B$, $C$, $D$, $E$ pontok közül valók, és mindhárom oldala azonos színű. d) Igazolja (például indirekt módszerrel), hogy nincs olyan csúcsa az ötszögnek, amelyből legalább három azonos színű szakasz indul ki!
*Kombinatorika (Azonosító: mme_201910_2r07f )
a) Igazolja, hogy nincs olyan 2-nél nagyobb $n$ egész szám, melyre $\dbinom{n}{1}$, $\dbinom{n}{2}$ és $\dbinom{n}{3}$ (ebben a sorrendben) egy mértani sorozat egymást követő tagjai! b) Határozza meg azokat az 5-nél nagyobb $n$ egész számokat, melyekre $\dbinom{n}{4}$, $\dbinom{n}{5}$ és $\dbinom{n}{6}$ (ebben a sorrendben) egy számtani sorozat egymást követő tagjai!
*Kombinatorika (Azonosító: mme_201910_2r08f )
Egy kétszemélyes társasjátékot olyan négyzet alakú táblán játszanak, amelyet fehér és szürke mezőkre osztottak fel az ábra szerint. 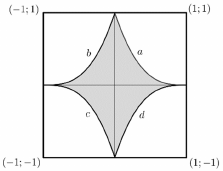
Ha a táblát egy olyan koordináta-rendszerbe helyezzük, amelyben a négyzet csúcsainak koordinátái $(1; 1)$, $(–1; 1)$, $(–1; –1)$, illetve $(1; –1)$, akkor ebben a koordináta-rendszerben az a jelű ív egyenlete: $y = (1 - x )^3$, $ 0 \le x \le 1$. A tábla középpontosan és tengelyesen is szimmetrikus. a) Írja fel a másik három (az ábrán b, c, illetve d jelű) ív egyenletét is! A társasjáték gyártója a 2 dm oldalú tábla fehér színű részének bevonásához egy speciális anyagot használ. Ebből 1 kg mennyiség 12 $m^2$ terület bevonásához elegendő. b) Számítsa ki, hogy 4000 darab tábla elkészítéséhez hány kg speciális anyag szükséges! A kétszemélyes társasjátékban minden játszma csak valamelyik játékos győzelmével végződhet, döntetlen nincs. Minden játszmában 1 pontot kap a győztes, a vesztes pedig 0 pontot. Anna és Bori nagyon szereti ezt a társasjátékot, sok játszmát lejátszottak már. Ha egymás ellen játszanak, akkor Anna 0,4 valószínűséggel, Bori pedig 0,6 valószínűséggel nyer meg egy játszmát. Egyik alkalommal megállapodnak, hogy addig játszanak újabb játszmákat, amíg valamelyikük először éri el a 10 pontot (és így megnyeri a játékot). c) Mennyi annak a valószínűsége, hogy Bori legfeljebb 12 játszma után megnyeri a játékot? (Kezdéskor mindkettőjüknek 0 pontja van.)
*Kombinatorika (Azonosító: mme_201910_2r09f )
Egy középiskolában a tizedikesek évfolyamdolgozatot írtak matematikából. A dolgozatban maximálisan 100 pontot lehetett elérni. Az évfolyamra járó 80 tanuló közül a dolgozat megírásakor néhányan hiányoztak. A dolgozatokban elért pontszámok átlagát először úgy számították ki, hogy a hiányzó tanulók eredményét 0 pontosként vették figyelembe. Rövid időn belül észrevették, hogy ez a számítási mód hibás. A hibát kijavították, így a hiányzók figyelembe vétele nélkül kapott átlag 4,2 ponttal magasabbnak adódott, mint az első (hibás) számítás utáni átlag. Egy héttel később az első megírás alkalmával hiányzó tanulók pótolták a dolgozatot; az ő átlageredményük 64 pont lett (a pótdolgozatban is maximálisan 100 pontot lehetett elérni). A teljes tizedik évfolyam matematika-évfolyamdolgozatainak átlageredménye így 67 pontos lett. a) Hány tanuló hiányzott a dolgozat első megírásakor? Hány pont volt azoknak a tanulóknak a helyesen számolt átlageredménye, akik az első alkalommal megírták a dolgozatot? Az évfolyamdolgozat egyik feladatában öt feleletválasztós kérdésben kellett négy-négy válaszlehetőség közül az egyetlen helyeset kiválasztani. Amikor Domonkos elolvasta a kérdéseket, akkor látta, hogy az első két kérdésre biztosan tudja a helyes választ (ezeket be is jelöli majd). A harmadik és a negyedik kérdésnél egy-egy válaszlehetőségről, az ötödik kérdésnél pedig két válaszlehetőségről tudta biztosan, hogy azok rosszak. Ezért úgy döntött, hogy az utolsó három kérdésnél tippelni fog: véletlenszerűen választ azon válaszlehetőségek közül, amelyekről nem tudja biztosan, hogy rosszak. b) Határozza meg Domonkos helyes válaszai számának várható értékét!
|
|


