Ha $ A = 1 111 111 111 $ és $ B = 111 111 $, akkor mennyi $ A $ és $ B $ legnagyobb közös osztója?
Mennyi az $f(x)=|x^2-x|+|x^2+3x+2|$ függvény legnagyobb és legkisebb értéke a $\left[-\dfrac{3}{2};\dfrac{1}{2}\right]$ zárt intervallumon? Mely helyeken veszi fel ezeket az értékeket?
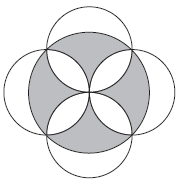
Mekkora a színezett részek területeinek összege, ha a kis körök sugara r?
Legyen $A=\dfrac{1}{2-\sqrt{3}}$, $B=\left(\sqrt{5}-\sqrt{2\sqrt{3}}\right)\left(\sqrt{2\sqrt{3}}+\sqrt{5}\right)$, $C=\sqrt{7-4\sqrt{3}}$. Bizonyítsuk be, hogy a $K=\sqrt{(A+B-C)\cdot n +2}$ kifejezés értéke minden n természetes szám esetén irracionális!
Egy kocka csúcsait megcímkézzük az $ 1;\ 2;\ \ldots\ ;\ 8$ számokkal (minden címkét pontosan egy csúcsra írunk fel). A kocka egy lapjának értéke: a lapot határoló csúcsokon lévő számok összege. Legfeljebb mekkora lehet egy kocka legkisebb értékű lapjának értéke?


