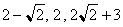
116. Egy adott számhármasból a következő módon “engedélyezett” képezni egy újabb számhármast: a három szám közül az egyiket nem változtatjuk, a másik kettőt pedig helyettesítjük a számtani és a mértani közepükkel. Megkapható-e “engedélyezett” lépések segítségével a számhármasból a

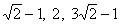
számhármas?
Megoldás

117. Az ABC egyenlőszárú derékszögű háromszög AC átfogóján úgy vettük fel az M és K pontokat, hogy K az M és C közé essék és, hogy az MBK

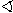45^o-os legyen.

Bizonyítsd be, hogy MK² = AM² + KC²!
Megoldás

118. Keress olyan természetes számot, amely a 2, 3, ... 10 számokkal elosztva mindig legalább feleakkora maradékot ad, mint az osztó! Melyik a legkisebb ilyen szám?
Megoldás

119.

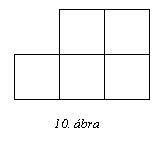
> A 10. ábrán látható alakzatot 5db 1x1-es négyzetből állítottuk össze. Ki lehet-e rakni ennek az alakzatnak az egybevágó példányaival egy 7x15-ös téglalapot?
Megoldás

120. A sakktáblán úgy helyeztünk el 11 lovat, hogy ne üssék egymást. Bizonyítsd be, hogy elhelyezhető még egy ló, hogy továbbra se üssék egymást!
Megoldás

121. Írd föl az 1995-öt a lehető legtöbb egymást követő természetes szám összegeként!
Megoldás

122. Határozd meg az n db kilencesből álló szám köbében a számjegyek összegét!
Megoldás

123. Fölírtuk sorban a táblára a természetes számokat 1-től 1995-ig. Először letöröljük a páratlan számokat. Ezután a megmaradtak közül letöröljük a páros helyen álló számokat, majd a megmaradtak közül újból a páratlan helyeken állókat töröljük le. Így haladunk tovább, amíg csak egyetlen szám nem marad. Melyik lesz ez a szám?
Megoldás

124. Az A, B, C, D természetes számokra teljesülnek az A + B = C + D = 1000 összefüggések. Határozd meg az

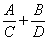összeg maximális értékét!

Megoldás

125. Az MNPQ paralelogramma M, N, P, Q csúcsai rendre az ABCD konvex négyszög oldalain helyezkednek el, mégpedig oly módon, hogy az egyes oldalakon AM : MB = BN : NC = CP : PD = DQ : QA = 1 : 2. Bizonyítsd be, hogy az ABCD négyszög is paralelogramma!
Megoldás

126. A Kozmosz expedíció bizonyos tagjai összevesztek és többé nem szóltak egymáshoz. A 11. ábrán látható táblázatba 1-est írtunk, ha a két űrutas még nem veszett össze és 0-t írtunk, ha már nincsenek beszélő viszonyban. A a rádiós megtudott egy földi hírt és továbbadta valakinek, akivel még beszélő viszonyban volt (tehát D-nek, vagy G-nek), aki szintén továbbadta valakinek, aki ... Végül mindenki megtudta az információt, legutoljára F kapta meg. Hogyan jutott el hozzá?

	A	B	C	D	E	F	G	H	I
A	-	0	0	1	0	0	1	0	0
B	0	-	1	1	1	1	1	1	1
C	0	1	-	0	0	0	1	1	0
D	1	1	0	-	1	0	1	0	1
E	0	1	0	1	-	0	1	0	1
F	0	1	0	0	0	-	0	0	1
G	1	1	1	1	1	0	-	0	0
H	0	1	1	0	0	0	0	-	0
I	0	1	0	1	1	1	0	0	-
11. ábra

Megoldás

127. Az ABCDE töröttvonal minden csúcsa illeszkedik egy előre adott körre (12. ábra).

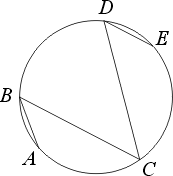
12. ábra

Az ABC, BCD és CDE szögek mind 45^o-osak. Bizonyítsd be, hogy AB² + CD² = BC² + DE²!

Megoldás

128.

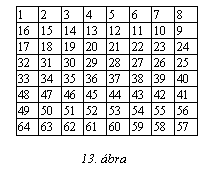
A sakktábla mezőit beszámoztuk a 13. ábrán látható módon. Helyezz király-nőket a táblára úgy, hogy ne üssék egymást, és a mezőiken levő számok összege a lehető legnagyobb legyen!
Megoldás

129. Bizonyítsd be, hogy tetszőleges egynél nagyobb k egész szám esetén meg lehet adni k db különböző pozitív egész számot úgy, hogy közülük bármelyik kettő szorzata osztható legyen a két szám különbségével.
Megoldás

130. Az l, m, n természetes számokra teljesül, hogy lm + ln = mn. Bizonyítsd be, hogy ekkor LNKO(l, m) + LNKO(l, n) = LNKO(m, n)!
Megoldás

131. Apa és fia körbe-körbe korcsolyáztak. Apa időnként megelőzte a fiát. Amikor a fiú elkezdett ellenkező irányban korcsolyázni, kiderült, hogy így ötször olyan gyakran találkoztak, mint előzőleg. Hányszor gyorsabban korcsolyázik az apa, mint a fia?
Megoldás

132. Egy 5 egység sugarú körbe írt négyzetet felosztottunk egymással egybevágó kisebb négyzetekre. Valamelyik két kis négyzetet elvéve, a maradék belefér egy 4 cm sugarú körbe. Igaz-e, hogy ilyenkor mindig elvehető még egy kis négyzet úgy, hogy a maradék elférjen egy 3 cm sugarú körben?
Megoldás

133. A császár udvarában körben 10 aranyszobor állt. Az uralkodó, aki a művészetek és a matematika nagy kedvelőjének tartotta magát, a körben szomszédos szobrok közé felfüggesztetett egy akkora gömböt, aminek a tömege megegyezett a két szobor tömegének különbségével. Az udvari matematikus azt állította, hogy e gömbök két csoportba oszthatók úgy, hogy a csoportokat egy kétkarú mérleg egy-egy serpenyőjébe téve azok épp kiegyenlítsék egymást. Igaza van-e?
Megoldás

134. Pelipáty és Kólinc városának sakkmérkőzésén mindkét csapatnak 1996 játékosa volt. A szervezők unalmasnak találták a szokásos módszert, amikor az egyik csapat első játékosa játszik a másik elsőjével, a második a másodikkal és így tovább. Elhatározták, hogy inkább úgy próbálják meg összepárosítani a játékosokat, hogy csapatbeli sorszámaik összege minden pár esetén négyzetszám legyen. Lehetséges-e ilyen párosítás?
Megoldás

135. Keresd meg a természetes számokból alkotható összes olyan x, y számpárt, amelyre teljesül az alábbi három feltétel:

3x y-nal osztva 1-et ad maradékul;

3y x-szel osztva 1-et ad maradékul;

xy 3-mal osztva 1-et ad maradékul.
Megoldás