Megoldások
Az 1995/96.
tanév
116. Vegyük észre, hogy ha az
(a?, b?, c?) számhármast az (a, b, c) számhármasból kaptuk,
akkor a?, b? és c? legkisebbike legalább akkora, mint
a, b és c legkisebbike.
117. Tükrözzük
A-t
BM-re,
C-t
BK-ra! Igazoljuk, hogy a két úton
ugyanahhoz a
D ponthoz jutunk! Bizonyítsuk be, hogy
MDK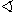
= 90
o!
118. A legkisebb ilyen szám az 599.
119. Ki lehet rakni.
120. Tekintsük a következő 12 mezőt:
a1, a2, b2, a8, b8, b7, g7, h7, h8, g1, g2, h1. Egy ló vagy ezek közül az
egyik mezőn áll, vagy támadja ezek közül az egyik mezőt, de egyszerre
mindkettőt nem teheti.
121. 1995 = 7 + 8 + 9 + ... +
63.
122. A számjegyek összege
18n. Érdemes a számot (10n – 1)3 =
103n - 3.102n +
3.10n – 1 alakba írni.
123. Ez a szám az 1366.
124. Az összeg maximumát pld. A =
D = 1, B = C = 999 esetén kapjuk.
125. I. megoldás: vektorokkal. II.
megoldás: Legyen M' az MB, P' a PD szakasz
fele-ző-pontja! Igazold, hogy a QPP', NMM' háromszögek
egybevágóak!
127. Megmutatjuk, hogy mindkét
négyzetösszeg a kör átmérőének négyzetével egyenlő. Az AC, BD és
EC húrok kerületi szögei 45o-osak, így középponti szögük
90o. Ha elforgatjuk a kör középpontja körül CD-t
90o-kal, akkor képe egy B-ből induló AB-re
merőleges húr lesz. Ezután használjuk Thalesz és Pithagorasz tételét!
128. 276 a legnagyobb összeg. Ezt
megkapjuk , ha a vezéreket a 6, 13, 23, 32, 40, 47, 53 és 62-es számú
mezőkre tesszük.
129. Megfelelő számokhoz jutunk, ha
k!-t rendre elosztjuk az 1, 2, ... k számokkal.
130. Legyen
l = ad, m= bd, n =
cd, ahol
a, b és
c relatív prímek, tehát
d az
l, m, n számok legnagyobb közös osztója. Ekkor
ab +
bc =
ac, amit
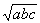
-vel
leosztva a
összefüggéshez jutunk.
Azt fogjuk megmutatni, hogy a fenti összefüggés tagjai rendre megegyeznek
LNKO(
a, b), LNKO(
b, c) és LNKO(
a, c) értékével.
Legyen pld.
e = LNKO(
a, c). Ekkor
e½
a
és
e½
c, de (
e,
b) = 1,
így
e2½
ac/
b. Másrészt, ha egy
p prím csak
a és
c egyikét osztja, akkor
p nem
osztja
a + c =
ac/
b-t, így
Ehhez hasonló lépésekkel befejezhető a
bizonyítás.
131. Másfélszer.
132. Igaz. Kiszámolható, hogy az 5
egység sugarú körbe írt négyzet 2 szomszédos csúcsán és az ezekkel
szemközti oldal felezőpontján áthaladó kör sugara nagyobb 4 cm-nél.
Ugyancsak nagyobb 4 cm-nél a négyzet két szomszédos oldalának
felezőpontján és az ezekkel szemközti csúcson áthaladó kör
sugara. Mindezek alapján belátható, hogy csak egy esetben teljesülhet
a feladat feltétele: ha négy egybevágó négyzetre osztottuk a négyzetet és
ezek közül két szomszédosat hagytunk el.
133. Legyenek M1, M2,
...M10 a szobrok tömegei; ekkor
|M1-M2|,
|M2-M3|, ... |M10
–M1| a gömbök tömegei. Az
(M1-M2) +
(M2-M3) +...+ (M10
–M1) = 0 azonosságban néhány zárójeles tag pozitív, a
többi pedig negatív (vagy nulla). Így a pozitív tagoknak megfelelő gömbök
össztömege megegyezik a negatívoknak megfelelőkével.
134. Lehetséges.
135. (2; 5) és (5;
2).