Az 1997. évi nyári tábor
feladatai
Egyéni verseny
(Olimpia)
T. 304 A táblán egymás mellett száz darab 7-es
látható. Plusz és mínusz jeleket helyezhetünk közéjük, ahová tetszik
(ahová nem teszünk jelet ott a számjegyek egy többjegyű számot
alkotnak). Lehet-e az így kapott kifejezés értéke
1997?
T. 305 Beírhatók-e az 1, 2, ..., 9 számok egy 3×3-as
táblázat mezőibe úgy, hogy bármelyik két (függőlegesen vagy vízszintesen)
szomszédos szám összege prímszám legyen?
T. 306 Bizonyítsd be, hogy minden konvex négyszöget
fel lehet darabolni négy olyan négyszögre, amelyek mindegyike
paralelogramma vagy trapéz!
T. 307 Az első Föld-Mars találkozón kiderült, hogy a
marslakók lába épp olyan, mint az embereké, de a kezek és rajtuk az ujjak
száma már más. Noha a marslakók hattal többen voltak, mint a földiek,
ujjaikból (a kezeket és s lábakat is figyelembe véve) összesen 1-gyel
kevesebb volt. Hány résztvevője volt az első találkozónak?
T. 308
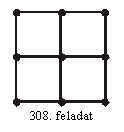 Rajzolj egy olyan minél
kevesebb oldalú önátmetszés nélküli zárt töröttvonalat, amely az ábrán
látható 12 szakasz mindegyikét metszi, de a 9 végpont egyikén sem megy át!
Rajzolj egy olyan minél
kevesebb oldalú önátmetszés nélküli zárt töröttvonalat, amely az ábrán
látható 12 szakasz mindegyikét metszi, de a 9 végpont egyikén sem megy át!
T. 309 Három versenyző egy köralakú biciklipályán megy
körbe-körbe, mindhárman állandó, de különböző sebességgel haladnak.
Tudjuk, hogy bármelyik két versenyző a pályának pontosan k helyén
találkozik egymással. Bizonyítsd be, hogy k páratlan szám!
T. 310 n erszény mindegyikében 20 érme van.
Külsőre mindegyik érme egyforma, de az egyik erszényben mindegyik érme 1
g-mal nehezebb, egy másik erszényben pedig mindegyik érme 1 g-mal
könnyebb, mint a többi érme, amelyek mind azonos tömegűek. Az érmék
tömegének három lehetséges értéke ismert. Mely n esetén lehet a
rugós-mutatós mérőműszer egyszeri használatával meghatározni, hogy mely
erszényekben milyen tömegű érmék vannak?
Szakkörök közti
vetélkedők
1. változat
T. 311 Van-e négy olyan különböző pozitív egész,
amelyek közül mindegyik osztható a másik három közül bármelyik kettő
különbségével?
T. 312 Hány megoldása van a 19[x] +
97{x} = 1997 egyenletnek? (Itt [x] az x egészrészét,
míg {x} a törtrészét jelöli.)
T. 313 Adott egy 4 m oldalú négyzetlap és egy 1 m
sugarú félkörlap. A félkörlap úgy mozog, hogy átmérőjének végpontjai
mindig a négyzetlapon vannak. Határozd meg annak az alakzatnak a
területét, amelyet a félkörlap végig tud söpörni?
Válaszoljunk a kérdésre abban az esetben is, amikor az átmérő két
végpontja csak a négyzet határoló vonalán mozoghat és a félkör mindig
befelé áll a négyzethez viszonyítva!
T. 314 Egy konvex négyszög belsejében fölvett pontot
összekötöttünk a négyszög csúcsaival. Így a négyszöget négy egybevágó
háromszögre osztottuk fel. Biztosak lehetünk-e benne, hogy a négyszög
rombusz?
T. 315 N cédulát megszámoztunk 1-től
N-ig, majd két csoportba osztottuk őket. Melyik az a legkisebb
N, amely esetén már biztosak lehetünk benne, hogy van két olyan,
azonos csoportban található cetli, amelyen a két szám összege négyzetszám?
T. 316 Lolka és Bolka pogácsát és fagylaltot vett.
Lolka 7 pogácsáért és 9 gombóc fagyiért több mint 20 petákot fizetett, míg
Bolka x pogácsáért és 16 gombóc fagyiért 42 petáknál kevesebbet
költött. x mely értékei esetén lehetünk biztosak benne, hogy egy
gombóc fagyi drágább egy pogácsánál, ha tudjuk, hogy a pogácsa nem olcsóbb
0,01 petáknál?
T. 317
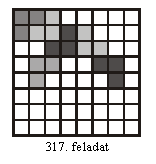
Bizonyítsd be, hogy akárhogy is helyezünk
el hat darab három mezőből álló "sarkot" a sakktáblán úgy, hogy
mindegyik lap pontosan három mezőt takarjon, mindig lesz közöttük
olyan, amelyiket el tudjuk mozgatni a táblán belül úgy, hogy a többi
lapot nem mozdítjuk meg.
T. 318 Amikor a ceruza már csak 2 centiméter hosszú,
csak egy "ceruzavég" maradt belőle, akkor pontos rajzolásra már
alkalmatlan, kidobják. Egy grafikus ceruzákat vett a papírboltban: 4
egyforma tízes csomag hosszú ceruzát, 6 egyforma doboz
közepes ceruzát (ezek 3 centiméterrel rövidebbek a hosszúaknál),
valamint 9 egyforma doboz rövid ceruzát (ezek feleakkorák,
mint a hosszúak). Utóbb kiderült, hogy a hosszú ceruzákkal összesen
ugyanannyit tudott rajzolni, mint a közepesekkel, és ugyanannyit, mint a
rövidekkel. Összesen hány centiméternyi ceruzavég keletkezett, ha tudjuk,
hogy mindegyik ceruza eredetileg legalább 5 centiméter volt?
2. változat
T. 319 Bizonyítsd be, hogy ha
a, b és
c
különböző egész számok, akkor
is egész szám!
T. 320
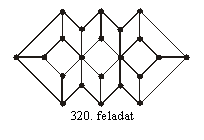
Az ábrán egy állam
városainak elhelyezkedése és a köztük épített utak hálózata látható. Be
lehet-e járni az állam városait az utakon úgy, hogy minden várost pontosan
egyszer keressünk föl?
T. 321 Két sokszög távolságán értsük ezentúl a két
sokszög területe összegének és közös részük területe kétszeresének
különbségét! Bizonyítsd be, hogy két sokszög távolsága nem lehet nagyobb,
mint egy harmadik sokszögtől való távolságaik összege!
T. 322 Tudjuk, hogy egy bizonyos n pozitív
egész számra az n3 | 3, n3 | 9,
n3 | 27, n3 | 81 állítások között van
igaz is, hamis is. Meg lehet-e ennek alapján mondani, hogy hány állítás
igaz a négyből?
T. 323 Egy háromszög beírt körének az oldalakkal való
érintési pontjain át párhuzamost húztunk a szemközti szög szögfelezőjével.
Mutassuk meg, hogy az így kapott három egyenes egy ponton megy át!
T. 324
 Felcserélhetjük egymással egy
táblázat bármelyik két sorát vagy bármelyik két oszlopát.
Megkapatóe ilyen műveletekkel az ábrán látható baldali
táblázatból a jobb oldali táblázat?
Felcserélhetjük egymással egy
táblázat bármelyik két sorát vagy bármelyik két oszlopát.
Megkapatóe ilyen műveletekkel az ábrán látható baldali
táblázatból a jobb oldali táblázat?
T. 325 Tekintsük az összes olyan valódi törtet, köztük
az egyszerűsíthetőket is, melyek nevezője legfeljebb 1997. Fel lehet-e
osztani ezeket két csoportra úgy, hogy a két csoportban az elemek száma,
és az elemek összege is egyenlő legyen egymással?
T. 326 Lewis Carrol ezt az elszámolást küldte
unokahúgának:
|
Font |
Schilling |
Penny |
|
Egy ellopott kesztyű |
|
2 |
0 |
|
A veszteség miatti fájdalom |
|
3 |
8,5 |
|
A fokozott nyugtalanság |
|
4 |
4,5 |
|
Az okozott kellemetlenség |
|
14 |
7 |
|
A tolvaj keresése miatti időveszteség |
|
1 |
6 |
|
ÖSSZESEN |
1 |
6 |
2 |
Meg lehet-e ennek alapján határozni, hogy egy font az hány schilling,
illetve egy schilling az hány penny, ha tudjuk, hogy egy font az több
schilling, mint ahány penny egy schilling?
3. változat
T. 327 Egy játék 1´1997-es táblájának mezői kezdetben
üresek és balról jobbra 1-től 1997-ig számozottak. A két játékosnál
egy-egy zsákban kellően sok figura van. A játékosok felváltva lépnek: egy
lépésben vagy fölteszik a zsákjukból kivett egyik figurát az egyik üres
mezőre, vagy átteszik bármelyik, már a táblán lévő bábút, a tőle jobbra
található legközelebbi üres mezőre (ha egyáltalán van ilyen). Az veszít,
aki nem tud lépni. Kinek van nyerő stratégiája, annak, aki kezd, vagy a
másik játékosnak?
T. 328 Bizonyítsd be, hogy
1994.1995×1996.1998×1999.2000 + 36
négyzetszám!
T. 329 Vágj szét két egyenessel egy előre adott
rombuszt négy olyan négyszögre, amelyekbe és amelyek köré is
írható kör!
T. 330 Egy kör kerületére 16 különböző pozitív egész
számot írunk és megjelöljük közülük azokat, amelyek egyenlők a két
szomszédjuk összegével. Legfeljebb hány számot jelölhetünk így meg?
T. 331 A "Szerelem első látásra" című műsorban nyolc
leány és nyolc fiatalember vett részt. Minden fiatalember a többi
résztvevő közül 14 emberrel, minden leány 7 emberrel veszett össze (az
összeveszések kölcsönösek). Bizonyítsd be, hogy a résztvevők közül
kialakítható 8 pár úgy, hogy a párok tagjai ne legyenek egymással
összeveszve!
T. 332 Öt párhuzamos húr a kört 10 ívre osztja.
Tudjuk, hogy bármelyik ív két szomszédja egymással egyenlő hosszú.
Bizonyítsd be, hogy a középső és a két szélső húr hosszának összege
egyenlő a további két húr hosszának összegével!
T. 333 Be lehet-e osztani 100 súlyt, melyek tömege 1,
2, 3, ..., 100 gramm, 10 csoportba úgy, hogy bármelyik két csoportban
különbözzön egymástól a súlyok össztömege, és a könnyebb csoportban mindig
több darab súly legyen, mint a nehezebben?
T. 334 Hány 13-mal osztható szám van az 1, 11, 111,
... számsorozat első száz tagja között?
Az elődöntő
feladatai
T. 335 Péter és Pál 13 cetlivel játszanak, amelyek meg
vannak számozva 1-től 13-ig. Kezdetben a cetlik mind az asztalon vannak.
Péter és Pál felváltva húznak közülük egyet-egyet, míg nem marad az
asztalon egy sem. Péter kezd és arra törekszik, hogy az általa kihúzott
cetliken a számok összege prímszám legyen. Meg tudja-e Pál ebben
akadályozni?
T. 336 Péter egy 10 cm oldalú négyzet belsejében egy 1
cm oldalú négyzetet helyezett el, amelynek oldalai a nagy négyzet
oldalaival párhuzamosak. Pál ki szeretné találni, hogy pontosan hol
helyezkedik el Péter kis négyzete. Ha Pál kijelöl egy tetszőleges
sokszöget, akkor Péter megmondja, hogy annak hány cm2 a kis
négyzettel való közös része. Elegendő-e két ilyen "kérdés" a kis négyzet
megtalálásához?
T. 337 Legfeljebb mekkorára növelhető az 1997 darab
1-est tartalmazó
1 + 1 × 1 + 1 . 1 + ... + 1 .
1
kifejezés értéke zárójelek ügyes elhelyezésével?
T. 338 A táblára föl volt rajzolva az y =
ax + b és az y = bx + a függvény
grafikonja. A táblát letörölték, csak a két grafikon ordinátatengellyel
való, illetve egymással vett metszéspontja látható. Hogyan lehetne
visszarajzolni az abszcisszatengelyt, ha tudjuk, hogy a ¹ b,
de a és b konkrét értékét nem ismerjük?
T. 339
 A 3.5-ös táblán
balról jobbra kell átjutnunk (ezért az első és az utolsó lépésnek
vízszintesnek kell lennie) úgy, hogy minden lépésben egy mezőről egy vele
oldalszomszédos másik mezőre léphetünk át, és egyik mezőre sem léphetünk
kétszer. Hányféleképpen lehetséges ez? Az ábrán egy
lehetőség látható a sok közül.
A 3.5-ös táblán
balról jobbra kell átjutnunk (ezért az első és az utolsó lépésnek
vízszintesnek kell lennie) úgy, hogy minden lépésben egy mezőről egy vele
oldalszomszédos másik mezőre léphetünk át, és egyik mezőre sem léphetünk
kétszer. Hányféleképpen lehetséges ez? Az ábrán egy
lehetőség látható a sok közül.
T. 340 Egy sorozatot a következőképpen adtak meg:
a1 = 19, a2 = 97,
an+2 = (an+1+
1)/ an, ahol n tetszőleges pozitív egész.
Határozd meg a1997 értékét!
T. 341 Az egyik évben három egymást követő hónap
mindegyikében négy vasárnap volt. Bizonyítsd be, hogy ezek közül az egyik
hónap biztosan február volt!
T. 342 Vannak-e olyan egymástól különböző
a, b, c,
d, e és
f pozitív egészek, amelyekre
a + b + c = d + e + f és a
. d = b × e = c . f
?
A döntő feladatai
T. 343 A C1, A1
és B1 pontok rendre az ABC háromszög AB,
BC és CA oldalain helyezkednek el, míg az
C2, A2 és B2 pontok
rendre az C1B, A1C
és B1A szakaszokon. Tudjuk, hogy a
C1A2,
C2B1 és az
A1B2 szakaszok egy ponton mennek át és
párhuzamosak az ABC háromszög oldalaival. Bizonyítsd be, hogy az
A1B1C1,
A2B2C2 háromszögek
területe egyenlő egymással!
T. 344

Egy 4
.4-es
táblázatban 16 szám volt. Az ábrán látható táblázatot úgy kaptuk az
eredetiből, hogy egy lépésben egyszerre minden számot helyettesítettünk a
sorában és oszlopában álló másik hat szám számtani közepével. Hogyan volt
kitöltve az eredeti táblázat?
T. 345 Legalább hányféle számjegyre van ahhoz szükség,
hogy megadjunk 16 olyan háromjegyű számot, amelyek közül bármelyik
kettőnek különböző a16-os maradéka?
T. 346 10 érme, melyek között van szabályos - 10
grammos -, és hibás - 9 grammos - is egymás mellé van téve. Tudjuk, hogy
minden szabályos érme balra van mindegyik hibás érmétől. Ki lehete
választani egy kétkarú mérleg kétszeri használatával, segédsúlyok
használata nélkül, a hibás súlyokat?
T. 347 Adj meg három háromszöget, amelyekből kirakható
(a darabok átfedése nélkül) háromszög is, konvex négyszög is, és konvex
ötszög is! (Az egyes összeállításokban mindegyik háromszöget föl kell
használni, és a háromszögeket el is lehet forgatni.)
T. 348 Azért, hogy meg tudja különböztetni őket Péter
két teljesen egyforma fehér kockán megjelölt 5-5 csúcsot egy-egy fekete
pöttyel. Bizonyítsd be, hogy Pál egy-egy pötty letör-lésével elérheti,
hogy a két kocka újra megkülönböztethetetlen legyen
egymástól!
T. 349 Bizonyítsd be, hogy az
x2×( z2 -
x2).( x2 -
y2) + y2.(
x2 - y2).(
y2 - z2) +
z2.( y2 -
z2).( z2 -
x2) £0
egyenlőtlenség bármely x, y, z számra teljesül!
T. 350 Egy üvegben egy amőbából 1997 keletkezett úgy,
hogy minden másodpercben vagy elpusztult egy amőba, vagy néhány amőba
mindegyike 6-6 amőbára osztódott. Legalább mennyi időre volt ehhez
szükség?
 Rajzolj egy olyan minél
kevesebb oldalú önátmetszés nélküli zárt töröttvonalat, amely az ábrán
látható 12 szakasz mindegyikét metszi, de a 9 végpont egyikén sem megy át!
Rajzolj egy olyan minél
kevesebb oldalú önátmetszés nélküli zárt töröttvonalat, amely az ábrán
látható 12 szakasz mindegyikét metszi, de a 9 végpont egyikén sem megy át! Rajzolj egy olyan minél
kevesebb oldalú önátmetszés nélküli zárt töröttvonalat, amely az ábrán
látható 12 szakasz mindegyikét metszi, de a 9 végpont egyikén sem megy át!
Rajzolj egy olyan minél
kevesebb oldalú önátmetszés nélküli zárt töröttvonalat, amely az ábrán
látható 12 szakasz mindegyikét metszi, de a 9 végpont egyikén sem megy át!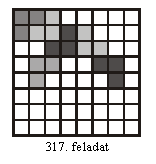

 Felcserélhetjük egymással egy
táblázat bármelyik két sorát vagy bármelyik két oszlopát.
Megkapatóe ilyen műveletekkel az ábrán látható baldali
táblázatból a jobb oldali táblázat?
Felcserélhetjük egymással egy
táblázat bármelyik két sorát vagy bármelyik két oszlopát.
Megkapatóe ilyen műveletekkel az ábrán látható baldali
táblázatból a jobb oldali táblázat? A 3.5-ös táblán
balról jobbra kell átjutnunk (ezért az első és az utolsó lépésnek
vízszintesnek kell lennie) úgy, hogy minden lépésben egy mezőről egy vele
oldalszomszédos másik mezőre léphetünk át, és egyik mezőre sem léphetünk
kétszer. Hányféleképpen lehetséges ez? Az ábrán egy
lehetőség látható a sok közül.
A 3.5-ös táblán
balról jobbra kell átjutnunk (ezért az első és az utolsó lépésnek
vízszintesnek kell lennie) úgy, hogy minden lépésben egy mezőről egy vele
oldalszomszédos másik mezőre léphetünk át, és egyik mezőre sem léphetünk
kétszer. Hányféleképpen lehetséges ez? Az ábrán egy
lehetőség látható a sok közül.