Megoldások
Az 1990/91.
tanév
1. Egyetlen egy ilyen szám
van, a 3 816 547 290.
2. a) I. megoldás: 1991 = 11
. 181, és az összeg mindkét tagja osztható 11-gyel, illetve
181-gyel.
II. megoldás: használjuk az alábbi átalakítást!
1.3.....1987.1989
= (1991 – 1990).(1991 – 1988).....(1991 –
4).(1991 – 2) =
1991.K -
1990.1988.....4.2
b) Alkalmazzunk
átalakítást az a) rész II. megoldásához hasonlóan!
3. Az első bolt 814, a második 1026,
a harmadik 150 könyvet adott el.
4. A keresett szám fölírható
A.100 + 56 alakban. 56 |
A.100, így 14 | A, azaz A páros és
osztható 7-tel, jegyeinek összege pedig 56-(5+6) = 45. A legkisebb olyan
páros szám, amelyben a jegyek összege 45 a 199998, de ez nem osztható
7-tel. A következő a 289998, majd a 298998. Ez utóbbi osztható csak 7-tel.
Tehát a keresett szám a 29899856.
5. a) Nem lehetünk biztosak
benne. Ha például a tábla 28 szélső mezőjén vannak a bábúk, akkor nem
tudunk elvenni belőlük úgy, hogy minden sorban és oszlopban csak 1-1
maradjon.
b) Biztosak lehetünk benne.
Tekintsük ugyanis azokat a zárt töröttvonalakat, amelyek csúcsai a bábúk,
oldalai pedig felváltva a sorokkal, illetve az oszlopokkal párhuzamosak.
Minden ilyen töröttvonalnak páros sok csúcsa van. Ha a töröttvonalak
minden második csúcsánál elhelyezett bábút levesszük, akkor minden sorban
és oszlopban 1-1 bábú marad.
6.

A bűvös négyzetet meghatározza három eleme (az ábrán
a,
b és
c). Ezek segítségével könnyen ellenőrizhető algebrai
azonosság alakjába írható át az állítás.
7. A második játékos győz.
Stratégiája: ellenfele által behúzott élnek a tábla középpontjára
vonatkozó szimmetrikus képét húzza be.
8. Ha mind az 1990 sorban előfordul
(-1)-es, akkor nyilvánvalóan teljesül az állítás. Egyébként tekintsük azt
a legelső sort, amelyben nincs (-1)-es! Ha ez a k-adik, akkor a
(k-1)-edik sorban szükségképpen mind az 1991-(k-1) szám
(-1)-es. Az ezt megelőző (k-2) sor mindegyikében pedig legalább egy
(-1)-es szerepel. Ez így már legalább 1991-(k-1) + (k-2) =
1990 db (-1)-es.
9. a) Nem. Vegyük észre, hogy
a és b legnagyobb közös osztója megegyezik (a-b) és
a, illetve a és (b-a) legnagyobb közös osztóival.
Tehát a szabály nem köt ki semmit olyan pontokról, amelyekben a két
koordináta legnagyobb közös osztója különböző.
b) Igen. Mindkét pont ugyanolyan
színű, mint a (0; 13) pont.
10. Mindkét esetben el lehet végezni
a mérést.
a) Az első két mérésnél nem
használunk súlyokat, hanem a lisztet megfelezzük a mérleg két
serpenyőjében. Így először 4500-4500 g lisztet kapunk, majd az egyik fél
megfelezésével 2250-2250 g-os adagokat kapunk. Ezek közül az egyikből
lemérünk 250 g-ot és megkapjuk a kívánt mennyiséget.
b) Ha fölrakjuk a 200 g-os súlyt az
egyik serpenyőbe és az összes lisztet elosztjuk a két serpenyőben, hogy
kiegyenlítsék egymást, akkor a "súlyos” serpenyőben 4400, a másikban 4600
g liszt lesz. A 4400 g-nyi liszt megfelezésével, majd 200 g liszt
elvételével a kívánt mennyiséghez jutunk.
11. Használjuk fel a háromszög
területképletét!
12. 987 654 321 – 123 456 789 = 864
197 532.
13. 9. Kezdjük a végén! Ha N
az unokák száma, akkor az N-edik unokának N, az
(N-1)-edik unokának pedig (N-1) + N/9 almát jutott. A
kapott almák egyenlőségéből N = 9 adódik.
14. 378. Ha a 10 számjegyből
kiválasztunk 5-öt, akkor ezekből pontosan egy csökkenő "Menő”
telefonszámot készíthetünk. Ezek száma tehát
A növekvő "Menő” számokban nem lehet 0,
ezért ezek száma
15. n = 1, és n =
3.
16. 267-féleképpen. A középső "V”
betűt kell elhagyni, hogy 145 lehetőség maradjon.
17. Még 3 traktorra van szükség.
Ha kezdetben a traktorok száma
t
volt, a szükséges napok száma
n, akkor
15.t.n = 300.
Az újabb traktorok segítségével 6 nappal
gyorsabban kellene végezni, azaz
15.(t +
u).(n – 6) = 300,
ahol
u jelöli az újonnan hozandó
traktorok számát. Az egyenletekben
n és (
n – 6)
a 20
olyan pozitív osztói, melyek különbsége 6, tehát a 10 és a 4. Ezért
t és (
t + u) 2 illetve 5, azaz még 3 traktorra van
szükség.
18. Két esetet kell
megkülönböztetni. Vagy
NBM
vagy
MNB
(vagy ezzel ekvivalensen
NMB
) a
60
o-os. Az első esetben a szögek számolásával igazolható az
ABN és
DBM háromszögek egybevágósága. A második esetben
megkeressük az
AB szakasz-nak azt a
K pont-ját,
amelyre
AK =
AN. Most a
DNM és
KBN háromszögek
egybevágóságát lehet igazolni.
19.
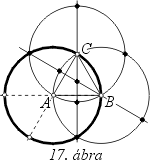
A
A kp-ú
AB sugarú kör bármely pontja -négy pont kivételével-
és még további 6 pont jó, amint az a 17. ábrán látható. (Részletesebben
lásd a Bergengóc példatárban a 82. feladat megoldását, a 152- 153.
oldalakon!)
20. Az egyes kupacokban található
gyufák száma az optimális esetben: 1, 14, 27, 40, 53, 65.
21. Jelölje ai
(i = 1, 2, ..., 8) az i-edik sorban álló bástya
oszlopának számát. A feladat megoldása az
1.a1 + 2.a2 +
... + 8a8 = 8.(9 – a1) +
7.(9 – a2) + ... + 1.(9 –
a8)
egyenlőség igazolásából áll.
22. 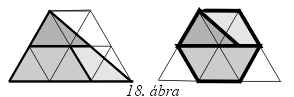
Lásd a 18. ábrát! Részletesebben lásd a Bergengóc példatárban a
64. feladat megoldását a 124-126. oldalakon.
23. Csak egy olyan számpár van, ami
megfelel mind a három feltételnek: 1 814 460, 1 814
340.
24. Bizonyítsd és használd a
következő segédtételt: a trapéz hosszabbik alapjának és egyik szárának
összege nagyobb, mint a rövidebbik alap és a másik szár összege!
25. Ez a szám az 1991.
26. Tegyük fel, hogy m-szer
vágtuk a papírt 6-felé és n-szer 12-felé, és így összesen N
papírdarabot kaptunk. Mivel minden ilyen vágásnál 5-tel, illetve 11-gyel
nőtt a darabok száma, így 1 + 5m + 11n = N. Ezt az
egyenletet kell vizsgálni N = 40, illetve N ³ 41 esetén.
27. Az öt szám: (-3); 2; 4; 5;
8.
 A bűvös négyzetet meghatározza három eleme (az ábrán a, b és
c). Ezek segítségével könnyen ellenőrizhető algebrai
azonosság alakjába írható át az állítás.
A bűvös négyzetet meghatározza három eleme (az ábrán a, b és
c). Ezek segítségével könnyen ellenőrizhető algebrai
azonosság alakjába írható át az állítás.  A bűvös négyzetet meghatározza három eleme (az ábrán a, b és
c). Ezek segítségével könnyen ellenőrizhető algebrai
azonosság alakjába írható át az állítás.
A bűvös négyzetet meghatározza három eleme (az ábrán a, b és
c). Ezek segítségével könnyen ellenőrizhető algebrai
azonosság alakjába írható át az állítás. 
