136. Egy sincs.

137. Azt érdemes felhasználni, hogy bármely ötágú csillagban az 5 konvex szög összege éppen 180^o.

138. 3 dollár és 61 cent.

139. Bontsd fel a zárójeleket!

140. Vizsgáljunk először három sorban egymás mellett elhelyezkedő gombot, azaz egy 3x1-es téglalapot! Nem nehéz megmutatni, hogy erre a téglalapra korlátozódva a kérdés megoldható: akárhogyan is rendeződtek el eredetileg a világító és a nem világító gombok, e három gomb közül egyeseket megnyomva elérhető, hogy e téglalap mindhárom gombja kialudjék.

Ezután bizonyítsunk hasonló állítást 3x3-as négyzetre! A fölső és az alsó sor gombjait használva hozzunk létre a középső sorra szimmetrikus helyzetet, majd ezt a tulajdonságot megtartva érjük el, hogy a két oldalsó sor kialudjék. Így összesen csak négyféle állapot jöhet létre, amely könnyen áttekinthető.

Ezeket az eredményeket fölhasználva 3x7-es téglalapra, végül a 7x7-es négyzetre igazoljuk az állítást.

141. Ha n páros, akkor mind az (n+2)^×(n+1)/2 dominó kirakható. Ha n páratlan, akkor (n-1)/2 dominó meg kell maradjon, maximum (n² + 2n + 3)/2 dominó rakható ki. Rész­le­tesebben lásd a Bergengóc példatárban a 109. feladat megoldását a 194-198. oldalakon.

142. Nincs ilyen szám: 0 = (-1) + 0 + 1; n = -(n – 1) + ... + (n – 1) + n.

143. Tekintsük a kört és 18 átmérőjét, melyek 36 egybevágó (10^o-os) körcikkre osztják a kört. Az egyik átmérő legyen párhuzamos vizsgált sokszögünk egyik oldalával. Így a sokszög mindegyik oldala párhuzamos a 18 átmérő egyikével. Mivel a sokszögnek 19 oldala van, ezért biztosan lesz kettő, amelyek ugyanazzal az átmérővel, tehát egymással is párhuzamosak.

144. Enikő a legöregebb. Ez egyébként, a rejtélyeskedő válasz alapján eleve sejthető volt.

145. a) Nem. Vizsgáljuk pld. azt az esetet, amikor a könyvek kezdetben csökkenő sorrendben helyezkednek el (a könyvek helyett a 8, 7, ...1 számokkal dolgozunk):

87654321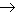65843217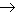84632175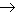63821754826175436187543287654321.

Egy olyan periodikus folyamatot kapunk, amelynek során az összehasonlításkor a bal szélső könyv mindig nagyobbnak adódik, mint a balról a második. Ugyanez lesz a hely­­zet, ha a folyamatot a periódus második tagjából indítjuk, tehát a 65843217 nagy­ságrendből.  Ezért a 6. és a 8. könyvek közül nem lehet logikailag kiválasztani a legnagyobbat. b) Nincs. Ahhoz, hogy nagyságrendi sorrendbe rakhassuk a könyveket az összes i < i+1 (i = 1, 2, ... 7) összehasonlítást el kell végezni. E hét összehasonlításból azon­ban legfeljebb hatra kerülhet sor.

146.

Vegyük észre, hogy 11711 és 11171111 osztható 7-tel, 7111 osztható 13-mal, 111111 pedig 7-tel és 13-mal is osztható. Az utolsó észrevétel alapján a szóbajöhető számokat érdemes az egyesek számának hatos maradéka szerint csoportosítani. Ha ez a maradék 2 vagy 5, akkor a szám osztható 3-mal, bárhol van benne a 7-es. Ha a hatos maradék 3, akkor tegyük a 7-est az ezresek helyére, így 13-mal osztható számot kapunk. Ha pedig az egyesek számának hatos maradéka 0, 4 illetve 1, akkor az a szám lesz biztosan 7-tel osztható, amelyikben a 7-es az egészek, a százasok, illetve a tízezresek helyén áll.

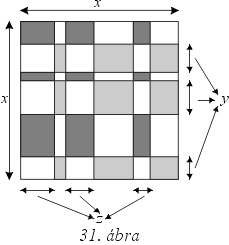
147. Legyen a négyzet oldalának hossza x. Adjuk össze minden második vízszintes sáv szélességét és minden páratlanadik függőleges sáv szélességét (lásd a 31. ábrát!). Ha az így kapott értékek y, illetve x, akkor a sötét részek összterülete

x²/2 = y(x-z)+(x-y)z.

Rendezés és szorzattáalakítás után a

(x-2y)(x-2z) = 0

egyenlethez jutunk. Tehát y és z közül legalább az egyik x/2-vel egyenlő. Innen már egyszerűen adódik a feladat állítása.

148. Ezek a 125^×10^k alakú számok, ahol k tetszőleges nem negatív egész szám.

149.

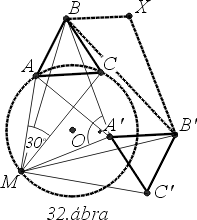
Forgassuk el M körül -60^o-kal az ABC háromszöget, illetve B körül 60^o-kal C-t, mint ahogy a 32. ábrán lát­ha­tó. A pontok képei legyenek A?, B?, C?, illetve X. Az A'B'B, CBM háromszögek egybevágóak, mert mind­ketten egybevágóak a XBB' háromszöggel. Az előbbit B körül kell 60^o-kal, az utóbbit BB' felezőpontja körül kell 180^o-kal forgatni, hogy XBB'-be jusson. Ezért A'B = MC. Az A'AB, MAC háromszögek egybevágóak, hiszen A körül egymásba forgathatóak. A kerü­leti szögek tétele miatt AMC = 30^o, így AA?B = 30^o. De AA'M szabályos háromszög, így MA'B derékszögű háromszög. A bizonyítandó állítás a Pithagorasz tételnek felel meg.

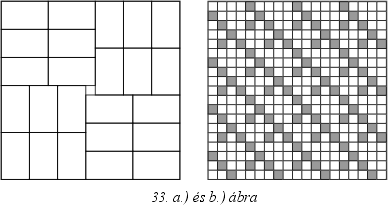
150. Vegyünk fel 24 db 3x5-üs téglalapot a 19x19-es négyzetben a 33.a) ábrán látható módon. Bizonyítsuk be, hogy ezek közül a téglalapok közül ez egyik biztosan megfelelő, nem lehet mindegyikben 3-nál több satírozott mező. A 33.b) ábrán látható 19x19-es négyzetben úgy festettünk be 96 mezőt, hogy bármely 3x5-ös téglalapban 4 vagy több mező lett befestve.

151. Mutassuk meg, hogy a k-adik (k = 1, 2, 3, ...) átlóban álló számok összege k^×(k+1)^×(k+2)/6.

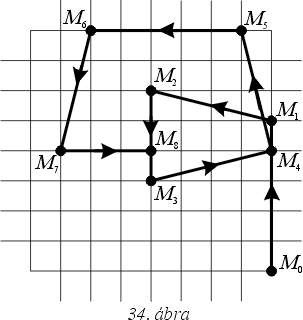
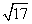
152. Az M által bejárt út (4+)a.  A 34. ábrán látható a felezőpont pályájának fele. Addig ábrázoltuk a pályát, amíg az A pont a kiindulási csúccsal szemközti csúcsba ér, tehát amíg a B pont másodszorra ér vissza kiindulási helyére. M akkor van pályájának töréspontjában, amikor B a négyzet egyik csúcsában jár.

153. Nem, ilyen módszerrel kapott kétjegyű szám biztosan osztható kilenccel.

154. Azt a 4x4-es négyzetet kell kivágni, amelynek középpontja a sakktábla középpontja is.

155. Bizonyítsuk be, hogy az öt kör középpontjait tartalmazó bármely szabályos háromszög oldalának hossza legalább 4 egység!