Megoldások
Az 1996. évi nyári tábor
feladatai
T. 226. Legyen a távolság
n km. Az első
kőoszlopnál az egyik szám 1, a másik szám pedig
n - 1. Mivel ezek
számjegyeinek összege 13, ezért
n - 1 számjegyeinek összege 12.
Ezért
n - 1
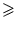
39,
tehát
n
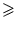
40.
Ha
n páros lenne, akkor a középső kőoszlopon két azonos szám állna,
így a számjegyeik együttes összege páros lenne, de 13 páratlan. Tehát
n páratlan, így utolsó számjegye nem lehet 0. Ezért
n - 1
számjegyösszege 1-gyel kisebb
n-énél, tehát
n
számjegyösszege 13. Ha
n legalább 60 lenne, akkor az 59. kőoszlopon
rajta lenne az 59, aminek már több 13-nál a számjegyösszege. Tehát
n legfeljebb 59 lehet. Keressük meg azokat az 59-nél nem nagyobb
pozitív egészeket, amelyek számjegyösszege 13. Ezek a 49 és az 58. Az 58
azonban páros,
n pedig páratlan. Tehát
n egyetlen lehetséges
értéke 49. Megmutatjuk, hogy a 49 egy jó megoldás. Vegyünk egy tetszőleges
kőoszlopot, legyen a rajta lévő két szám
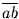
és
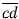
( 0
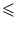 a
a,
b,
c,
d
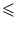
9).
Ekkor tudjuk, hogy
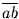
+
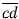
= 49
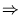
10
a +
b + 10
c +
d = 49, tehát
10(
a+
b) +
c +
d = 49. 0
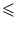 c
c +
d
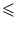
18
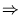
31
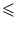
10(
a+
b)
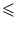
49
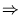 a
a +
b = 4
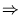 c
c +
d = 9, tehát
a +
b +
c +
d =
4 + 9 = 13.
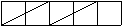
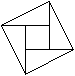
T. 227. Az első ábrán a vágások, a másodikon a
darabokból összeillesztett négyzet látható.
|
 |
|
|
1. ábra |
2. ábra |
T. 228.
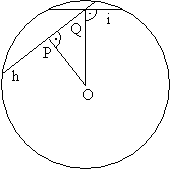
Legyen a kör középpontja
O. Vegyük a
legrövidebb húrt, legyen ez
h. Minél távolabb van egy húr a
középponttól, annál rövidebb. Legyen
P az
O-ból
h-ra
állított merőleges talppontja. Legyen
i egy olyan húr, amelyet
h felez. Legyen
i felezőpontja
Q. Ekkor
i húr
távolsága az
O-tól:
QO =
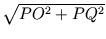
.
QO
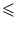 PO
PO
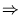 QO2
QO2
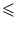 PO2
PO2
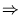 PO2
PO2 +
PQ2
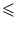 PO2
PO2
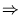 PQ2
PQ2
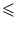
0
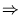 PQ
PQ = 0. Tehát
P pont két húr felezőpontja is.
O-n kívül nincs ilyen pont, ezért
h felezőpontja
O.
De ekkor
h átmérő, tehát minden húr átmérő.
T. 229.
Legyen egy közös pont
x koordinátája
x0. Ekkor a következőket
tudjuk:
ax0 +
b =
bx0 +
c =
cx0 +
a
c =
ax0 +
b -
bx0ax0 +
b =
(
ax0+
b-
bx0)
x0
+
a =
ax02 +
bx0 -
bx02 +
a
0 =
ax02 -
bx02 -
ax0 +
bx0 +
a -
b =
(
a-
b)
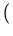 x02
x02-
x0+1
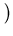 x02
x02 -
x0
+ 1 =
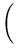 x0
x0-
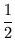
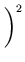
+
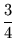
> 0
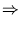 a
a -
b = 0
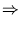 a
a =
b
ax0 +
a =
ax0 +
c
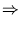 a
a =
cTehát
a =
b =
c.
T. 230. Nem tud biztosan erre rájönni.
Tegyük fel, hogy a hamis érme súlya egy jó érme súlyánál legfeljebb annak
egytizedével nagyobb vagy kisebb. Ha a két karra különböző számú érmét
rak, azzal semmilyen új információhoz nem jut. Tehát elég azokat a
méréseket vizsgálni, amelyekben a két karon azonos számú érme van. Ha a
hamis érme a mérlegen van, akkor az nincs egyensúlyban, és ha nincs rajta,
akkor egyensúlyban van. Minden mérésen páros számú érmét rak fel a
mérlegre. Ezért az első mérésben nem szerepel minden érme. Tegyük fel,
hogy az első mérésben csak jó érme szerepel. Ekkor egyensúly van, és
ezeket az érméket rögtön le kell adni. Így még páratlan sok érme marad. Ha
a következő lépésben is egyensúly lesz, akkor megint páratlan sok marad,
stb. Ekkor minden lépésben legalább 2-vel csökken az érmék száma, ezért
egy idő után már csak egy érme marad, ez pedig a hamis érme lesz. Tehát
megtudtuk, hogy melyik a hamis érme, de azt nem, hogy könnyebb vagy
nehezebb, mint egy jó érme.
T. 231. Egy szög szögfelezője azon pontok halmaza,
melyek egyforma távolságra vannak a két szögszártól. Ezért
M
egyforma távol van
AD és
AB ill.
AB és
BC egyenesektől,
N pedig a
BC és
CD ill.
CD és
AD egyenesektől. Tehát
M egyforma távol van
AD és
BC egyenesektől,
N pedig a
BC és
AD egyenesektől. Hosszabbítsuk meg
AD és
BC
oldalakat.
Ha ezek metszik egymást: Legyen a metszéspontjuk
E. Ekkor
M és
N a föntiek miatt rajta van az
AEB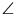
szögfelezőjén. Tehát
MN egyenes megegyezik
ezzel a szögfelezővel, ezért ez a szögfelező merőleges
AB-re.
ABE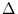
-ben az
E csúcsból induló szögfelező
merőleges
AB oldalra, tehát
EAB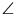
=
EBA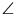
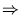 DAB
DAB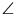
=
ABC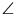
.
Ha ezek párhuzamosak: Ekkor
MN egyenes a
föntiek miatt
AD és
BC egyenesek középpárhuzamosa. Tehát
MN||
AD||
BC. Mivel
MN merőleges
AB-re, ezért
AD és
BC is merőleges
AB-re, tehát
DAB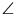
=
ABC
= 90°.
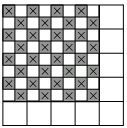
T. 232. A 32 megfelelő lövés az ábrán
látható. Vegyük a bal felső sarokban lévő 8×8-as négyzetet. Színezzük ki
ezt sakktáblaszerűen. A sötét mezők azok, amelyekre lövünk. Ha egy hajó
mindkét négyzete benne lenne ebben a 8×8-as négyzetben, akkor a két
négyzet színe különböző lenne, így valamelyik sötét lenne, tehát a hajót
eltalálnánk. Így ahhoz, hogy semelyik hajót ne találjuk el, minden hajónak
kell lennie olyan négyzetének, amely a 8×8-as négyzeten kívül van. Osszuk
fel a kívül lévő részt 9 db 2×2-es négyzetre. Egy ilyen 2×2-es négyzetben
bármely két négyzet szomszédos, ezért egy ilyen négyzetnek legfeljebb egy
hajóval van metszete. De több hajó van, mint 2×2-es négyzet, ezért ezt nem
lehet megvalósítani, így biztosan lesz olyan hajó, amit eltalálunk.
T. 233. Nem lehetséges. Száz szám között vagy egy,
vagy kettő olyan van, amelyik osztható 64-gyel. Ha egy van, akkor az csak
az egyik csoportban van benne, így itt a legkisebb közös többszörös
osztható 64-gyel, míg a másik csoportnál nem. Ha kettő van, akkor ezek
egyike osztható 128-cal, a másik nem, így az egyik csoportnál a legkisebb
közös többszörös osztható 128-cal, a másiknál pedig
nem.
T. 234.
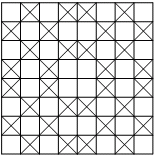
Vegyünk két egy sorban vagy oszlopban lévő mezőt, amelyek
között három mező van. Tegyük fel, hogy a 2 mező egyikén sincs detektor.
Ezen az 5 hosszúságú téglalapon kétféle hajó is lehet. Mivel nincs olyan
detektor, amely a két hajó közül csak az egyiken van rajta, ezért nem
tudjuk meghatározni a hajó pontos helyzetét. Tehát bármely ilyen helyzetű
mezők esetén a 2 mező közül legalább 1 mezőn detektornak kell lennie.
Ezért az 1. és 5., a 2. és 6., a 3. és 7., a 4. és 8. sorokban legalább
8-8 detektor van. Így összesen legalább 32 detektorra van szükség. Ennyi
detektor már valóban elég is, itt egy példa, ahol a detektorok úgy vannak
elhelyezve, hogy mindig meg tudjuk határozni a hajó helyzetét.
T. 235. Tegyük fel, hogy lehetséges a feladat
állítása. Legyen a legkisebb kitevőjű hatvány a 3a. Az
összes többi hatvány 3a . 3b
alakú, ahol b természetes szám. Így a hatványok összege megegyezik
egy szorzattal, melynek egyik tényezője a 3a, a másik
pedig 1000 páratlan szám összege, ami páros. Ha a nem negatív,
akkor a szorzat páros szám. Ha a negatív, akkor egy páros számot
elosztunk egy páratlan számmal, tehát vagy páros számot, vagy nem egész
számot kapunk. Így 3333 nem lehet a hatványok összege.
T. 236. A következő egyenletrendszert kell
megoldanunk:
ax + by + c = 0
bx + cy +
a = 0
cx + ay + b = 0
x >
0, y > 0
Az első három egyenletet
összeadva ezt kapjuk: (a+b+c)(x+y+1) =
0
 a + b + c = 0. Ebből c = -
a - b, így a három új egyenlet:
a + b + c = 0. Ebből c = -
a - b, így a három új egyenlet:
ax + by
- a - b = 0
bx - ay - by + a
= 0
- ax - bx + ay + b = 0
Az utolsó két egyenletből:
x(a + b) =
ay + b
y(a+b) = bx +
a
Ha a + b = 0: a és b egyszerre
nem lehet 0, mert ekkor c is 0, és ekkor nem egyenesekről lenne
szó. Egyébként b = - a-t behelyettesítve:
- ax
- ay + ay + a = 0
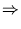 ax = a
ax = a
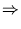 x = 1
x = 1
- ax + ax + ay - a = 0
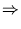 ay = a
ay = a
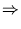 y = 1
y = 1
Tehát az (1; 1) pont egy lehetséges megoldás.
Ha a + b
0:
x =
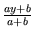 és
y =
és
y =
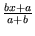 , ezért x =
, ezért x =
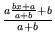 =
=
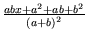 = 1 +
= 1 +
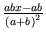 =
= 1 + (x-1)
=
= 1 + (x-1)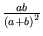
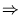 x - 1 = (x-1)
x - 1 = (x-1)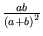 .
.
Ez csak kétféleképpen lehetséges: vagy x - 1 = 0, vagy
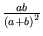 = 1. A második eset nem lehetséges, mert ekkor ab =
= 1. A második eset nem lehetséges, mert ekkor ab =
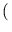 a+b
a+b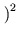 =
a2 + b2 + 2ab
=
a2 + b2 + 2ab
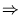 0 =
a2 + b2 + ab, de az utolsó
összeg minden tagja nem negatív, ezért mindegyik 0. De tudjuk, hogy ez nem
lehetséges. Tehát x = 1, így y =
0 =
a2 + b2 + ab, de az utolsó
összeg minden tagja nem negatív, ezért mindegyik 0. De tudjuk, hogy ez nem
lehetséges. Tehát x = 1, így y =
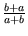 = 1.
Tehát most is az (1, 1) pont a megoldás.
= 1.
Tehát most is az (1, 1) pont a megoldás.
Valóban létezik három ilyen
egyenes, pl. az a = 1, b = - 1, c = 0 esetben.
T. 237. Legyen
AA1 és
CC1 felezőmerőlegeseinek a metszete
D.
AA1D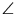
=
A1AD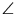
=
A1AB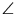
,
ezért
A1D||
AB. Ugyanígy
C1D||
BC. Ezeket és a szögfelezőtételt
használva ezt kapjuk:
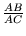
=
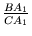
=
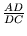
=
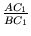
=
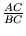
,
tehát
AC2 =
AB . BC.



![]() a + b + c = 0. Ebből c = -
a - b, így a három új egyenlet:
a + b + c = 0. Ebből c = -
a - b, így a három új egyenlet:![]() ax = a
ax = a
![]() x = 1
x = 1![]() ay = a
ay = a
![]() y = 1
y = 1 ![]() és
y =
és
y =
![]() , ezért x =
, ezért x =
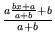 =
=
![]() = 1 +
= 1 +
![]() =
= 1 + (x-1)
=
= 1 + (x-1)![]()
![]() x - 1 = (x-1)
x - 1 = (x-1)![]() .
.
![]() = 1. A második eset nem lehetséges, mert ekkor ab =
= 1. A második eset nem lehetséges, mert ekkor ab =
![]() a+b
a+b![]() =
a2 + b2 + 2ab
=
a2 + b2 + 2ab
![]() 0 =
a2 + b2 + ab, de az utolsó
összeg minden tagja nem negatív, ezért mindegyik 0. De tudjuk, hogy ez nem
lehetséges. Tehát x = 1, így y =
0 =
a2 + b2 + ab, de az utolsó
összeg minden tagja nem negatív, ezért mindegyik 0. De tudjuk, hogy ez nem
lehetséges. Tehát x = 1, így y =
![]() = 1.
Tehát most is az (1, 1) pont a megoldás.
= 1.
Tehát most is az (1, 1) pont a megoldás.