Az 1996. évi nyári tábor
feladatai
Egyéni verseny
(Olimpia)
T. 226 A Pelipáty és Kólinc közötti országút minden
kilométerénél egy-egy kis kőoszlop áll az út szélén. Ennek egyik, illetve
másik oldalára az van írva, hogy hány kilométer van még Pelipátyig,
illetve Kólincig. Boriska észrevette, hogy a számjegyek összege minden
kilométerkövön 13. Mennyi az út Pelipátytól Kólincig?
Megoldás
T. 227 Vágd szét az 1×5-ös téglalapot 5 részre úgy,
hogy a darabokból négyzetet lehessen összeállítani!
Megoldás
T. 228 Berajzoltuk egy kör néhány (véges sok) húrját
úgy, hogy mindegyik húr átmenjen valamelyik másik húr felezőpontján.
Bizonyítsd be, hogy ez csak úgy lehetséges, hogy mindegyik húr átmérő!
Megoldás
T. 229 Az
a, b, c számok olyanok, hogy az
y
= ax +b, y = bx + c, y = cx + a
függvények grafikonjának van közös pontja. Bizonyítsd be, hogy
a = b = c!
Megoldás
T. 230 Kopasz kupec kasszájában hosszú idő óta
először pénz gyűlt össze, 99 érme. Tudni lehet sajnos, hogy az egyik érme
hamis, súlya különbözik a többiétől, amelyek viszont mind jók és egyforma
nehezek. Az alkalmazottak már régóta nem kapták meg járandóságukat és most
felháborodva követelik, hogy azonnal kapják meg bérüket a jó érmékből. A
kupec intézőjénél egy kétkarú mérleg van, de súly nincs nála. Ahogy
kiderül valamelyik érméről, hogy jó, akkor azonnal ki kell adni
fizetésként, a további mérésekben már nem vehet részt. A kíváncsi intéző
szeretné megtudni, hogy a hamis érme könnyebb- vagy nehezebb-e, mint a
szabályos érmék. Biztosan rá tud erre jönni?
Megoldás
T. 231 Az
ABCD konvex négyszög
A-nál és
B-nél lévő belső szögeinek szögfelezői az
M, a
C-nél
és
D-nél fekvő belső szögek szögfelezői az
N pontban metszik
egymást. Tudjuk, hogy az
M és
N pontok különbözők, és az
MN egyenes merőleges
AB-ra. Bizonyítsd be, hogy az
A-nál és
B-nél fekvő szögek egyenlők!
Megoldás
T. 232 A Torpedó játékban egy 10×10-es táblán kell
elhelyezni a 10 hajóból álló "hajórajt”. Egy hajó a tábla egy 1×2-es
téglalapja, a különböző hajóknak megfelelő téglalapoknak nem lehet közös
pontja, még közös oldala, csúcsa sem. Bizonyítsd be, hogy 32 megfelelően
választott "lövéssel” biztosan el lehet találni legalább egy hajót!
Megoldás
T. 233 50 természetes szám legkisebb közös
többszöröse megegyezik 50 másik természetes szám legkisebb közös
többszörösével. Lehetséges-e, hogy ez a száz szám 100 egymást követő
természetes szám?
Megoldás
Szakkörök közti
vetélkedők
1. változat
T. 234 A Torpedó játék egyik változatát 8×8-as táblán
játsszák. Erre az egyik játékos egy "hajót”, azaz egy 1×4-es téglalapot
rak. A másik játékos - a hajó helyzetét nem ismerve – detektorokat
helyezhet el a tábla mezőire, amelyek jelzik, hogy az adott mezőn van-e
hajó vagy nincs. Legkevesebb hány detektort kell elhelyezni ahhoz, hogy
egyértelműen meg lehessen határozni a hajó pontos elhelyezkedését,
akárhová is tette azt az első játékos?
Megoldás
T. 235 Lehet-e 3 – nem feltétlenül különböző – egész
kitevős hatványai közül ezernek az összege éppen 3333?
Megoldás
T. 236 Az
ax + by + c = 0 , bx + cy +
a = 0 , cx + ay + b = 0 egyenesek a pozitív síknegyedben,
egy közös pontban metszik egymást. Határozd meg a metszéspont koordinátáit
(figyelembe véve az összes lehetőséget)!
Megoldás
T. 237 Az
ABC háromszög
AA1,
CC1 szögfelezőinek felezőmerőlegese az
AC oldalon
metszi egymást. Bizonyítsd be, hogy
AC 2 =
AB × BC!
Megoldás
T. 238 Péter számokat ír a táblára: az életkorával
kezdi (években számolva), és a következő számot mindig úgy kapja, hogy az
előzőhöz hozzáadja annak legnagyobb számjegyét. Fel fogja-e valaha írni
10...096-ot (ahol az 1-es és a 9-es között 1996 nulla van)?
Megoldás (DOC),
Megoldás (PDF)
T. 239 Gabiék
fürdőkádja a melegvizes csapból 23 perc alatt, a hidegvizesből 17 perc
alatt telik meg. Gabi először a melegvizes csapot nyitotta meg. Mennyi
idő múlva engedje meg a hidegvizes csapot, ha azt akarja, hogy 1,5-szer
annyi kerüljön a kádba a melegvízből, mint a hidegből, amikor az éppen
megtelik?
Megoldás (DOC),
Megoldás (PDF)
T. 240 A diákok 17 kétjegyű pozitív egész számot
írtak a táblára. Kiderült, hogy az egyik szám századik hatványa osztható a
17 szám mindegyikével. Bizonyítsd be, hogy ebben az esetben az is igaz,
hogy ez a hatvány osztható a 17 szám szorzatával is!
Megoldás (DOC),
Megoldás (PDF)
T. 241 Bergengóciában olyan az úthálózat, hogy minden
út egyenesen halad egyik városból egy másikba, az utak egymást nem
keresztezik, és bármelyik városból bármelyik másikba el lehet jutni
nyílegyenesen, esetleg más, közbeeső városokon áthaladva. Igaz-e, hogy
Bergengócia mindegyik városa – egy vagy két kivételtől eltekintve – egy
egyenesen helyezkedik el?
Megoldás (DOC),
Megoldás (PDF)
2. változat
T. 242 a,
b és
n olyan
természetes számok, amelyekre
a96 +
b96 és
a100 +
b100
is osztható
n-nel.
Bizonyítsd be, hogy
a1996 +
b1996
is osztható
n-nel!
Megoldás (DOC),
Megoldás (PDF)
T. 243 Az
ABCD derékszögű trapéz
AB
magasságának hossza egyenlő a
AD,
BC alapok hosszának
összegével. Bizonyítsd be, hogy az
ABC szög szögfelezője megfelezi
a
CD oldalt!
Megoldás (DOC),
Megoldás (PDF)
T. 244 Egy 5×5-ös táblázat mezőibe úgy írtuk be az 1,
2, ..., 25 számokat, hogy bármelyik két egymás után következő szám
egymással szomszédos mezőbe került (olyanokba, amelyeknek van közös
oldala). Legfeljebb hány prímszám kerülhetett egy sorba?
Megoldás (DOC),
Megoldás (PDF)
T. 245 A
SOK + SOK + ... + SOK= ELÉG
számrejtvényben a
különböző betűk különböző, az azonos betűk azonos számjegyeket jelölnek.
Legfeljebb hány "SOK" adhatja ki az "ELÉG"-et?
Megoldás (DOC),
Megoldás (PDF)
T. 246 Ki lehet-e jelölni az 1996×1996-os
négyzetrácsban néhány kis négyzetet úgy, hogy bármelyik két olyan
1000×1000-es négyzetben, amelynek oldalai az eredeti rács egyenesein
vannak, különböző számú megjelölt kis négyzet legyen?
Megoldás (DOC),
Megoldás (PDF)
T. 247 Gyáva Oroszlán és Bádogember ugyanazon a napon,
ugyanazon az úton, ugyanabban az irányban indultak el, hogy eljussanak
Smaragdvárosba. Kezdetben Bádogember 100 mérföldre volt a céltól, 28
mérfölddel távolabb, mint Gyáva Oroszlán. Mindketten reggel 8-tól este
8-ig voltak úton, és egy napon belül mindig állandó volt a sebességük.
Bádogember az első nap 20, a másodikon 18, a harmadikon 16 km-t tett meg,
és így tovább, míg a Gyáva Oroszlán 4 km-rel kezdte, de a másodikon már 8
km-t haladt, a harmadikon 12-őt, és így tovább. Hol és mikor találkoztak
egymással?
Megoldás (DOC),
Megoldás (PDF)
T. 248 Adott 25 pozitív egész, melyek egyike sem
nagyobb 1000-nél. Tudjuk, hogy közülük bármelyik kettő szorzata
négyzetszám. Bizonyítsd be, hogy mind a 25 szám
négyzetszám!
Megoldás (DOC),
Megoldás (PDF)
T. 249 A
PIFAGOR és
TEOREMA szavakban az azonos betűk azonos, a
különböző betűk különböző számjegyeket jelölnek. Egy szóban két szomszédos
betűnek megfelelő számpárt rendetlennek nevezünk, ha a bal oldali szám
nagyobb a jobb oldalinál. Legkevesebb hány rendetlen számpár van összesen
a két szóban?
Megoldás (DOC),
Megoldás (PDF)
3. változat
T. 250 Kovács - a házfelügyelő - szedi össze a pénzt a
lakóktól a lakásokra kitett új számok miatt. Szabó azt szeretné megtudni
tőle, hogyan lehetséges, hogy nekik, a harmadik lépcsőházban, összesen
20%-kal többet kell fizetniük, mint a második lépcsőházban lakóknak
összesen, pedig mindegyik lépcsőházban ugyanannyi lakás van. Kovács nem
jön zavarba, elmagyarázza, hogy a kétjegyű számokért kétszer, a
háromjegyűekért háromszor annyit kell fizetni, mint az egyjegyűekért. Hány
lakás van egy lépcsőházban?
Megoldás (DOC),
Megoldás (PDF)
T. 251 A tanár az
a1x + a2 =
0, a2x + a3 =
0, a3x + a4 =
0, a4x + a5 =
0, a5x + a1 =
0
egyenleteket, és a
0,1; 0,2; 0,3; ... ; 0,9; 1; 1,1; ... ; 2
számokat írta a táblára. Azt mondta, hogy mindegyik egyenletnek egy-egy
megoldása van, ami megtalálható a felírt számok között. Péter szerint
ez lehetetlen. Igaza van-e?
Megoldás (DOC),
Megoldás (PDF)
T. 252 A számegyenesen megjelöltük az 1, 2, 3, ... ,
99, 100 számokat. Egy szöcske az 1-ről indulva 99-et ugrott, minden
megjelölt számjegyet pontosan egyszer keresett föl és legvégül 100-ra
érkezett. Lehetséges-e, hogy ugrásai hosszának összege épp 1996?
Megoldás (DOC),
Megoldás (PDF)
T. 253 Egy olyan körmérkőzéses focibajnokságot
vizsgálunk, amelyben bármely két csapat pontosan egyszer játszik
egymással, a győzelemért 3, a döntetlenért 1, a vereségért 0 pont jár.
A bajnokság végén, az pontszámok kiszámolása után egy mérkőzést
érdekesnek nevezünk, ha az a csapat nyert, amelyiknek kevesebb pontja
lett, érdektelennek pedig az olyan mérkőzést nevezzük, amelyet a több
pontszámot elért csapat nyert meg. Lehetséges-e, hogy a bajnokságban több
érdekes mérkőzés volt, mint érdektelen?
Megoldás (DOC),
Megoldás (PDF)
T. 254 32 (1×2-es) dominóval egy (8×8-as) négyzetet
raktunk ki. Bizonyítsd be, hogy a dominók kifesthetők úgy, hogy közülük 8
piros, 8 kék, 8 zöld és 8 sárga legyen, és semelyik két azonos színű
dominónak se legyen közös határvonala (legfeljebb csak a sarka)!
Megoldás (DOC),
Megoldás (PDF)
T. 255 Mennyit kapunk eredményül, ha összeadjuk azokat
az 1000-nél nem nagyobb pozitív egész számokat, amelyekben a számjegyek
összege páratlan?
Megoldás (DOC),
Megoldás (PDF)
T. 256 Adott az egységnyi oldalhosszúságú
ABCD
négyzet, és az
AB, BC, CD, DA oldalakon a
K, L, M, N
pontok úgy, hogy
AK + AN + CL + CM = 2. Bizonyítsd be,
hogy a
KM és az
LN szakaszok merőlegesek egymásra!
Megoldás (DOC),
Megoldás (PDF)
T. 257 Születésnapja alkalmából Leonhard Euler
megkínálta barátait egy háromszög alakú tortával, amelyet a
szögfelezők mentén vágva hat részre darabolt föl. A késve érkező
Münchausen bárónak maradt az utolsó szelet, amely
derékszögű háromszög alakú volt. A szelet alakja alapján a báró
kijelentette, hogy a torta csakis egyenlő szárú háromszög alakú lehetett.
Igaza volt-e?
Megoldás (DOC),
Megoldás (PDF)
4. változat
T. 258 Bizonyos egész számokat
jónak nevezünk.
Ismeretes, hogy az 1000 jó szám, és hogy ha 53
x + 54
y jó
szám, akkor 54
x + 53
y is az (
x és
y
tetszőleges egész számok). Bizonyítsd be, hogy 1996 is jó
szám!
Megoldás (DOC),
Megoldás (PDF)
T. 259 1996 diót 20 nem üres kupacba osztottunk. Át
szabad tenni egy diót az
A kupacból a
B kupacba, ha
A-ban több mint 1 dió van és az
A-beli diók száma osztható a
B-beli diók számá-val. Bizonyítsd be, hogy a kupacok ilyen
rendezéseivel elérhető, hogy a 20 kupac mindegyikében legalább 3
dió legyen!
Megoldás (DOC),
Megoldás (PDF)
T. 260 Péter és Pál egy-egy egymással egybevágó
sokszögalakú papírlapot kapott. Sokszöglapjukat mindketten
fölosztották egy-egy vonal mentén két részre, és az egyiket pirosra, a
má-sikat kékre festették. Kiderült, hogy a két kék rész is egybevágó
egymással és a két piros is. Igaz-e, hogy a két eredeti sokszöglapba Péter
és Pál által berajzolt két vonal is egybevágó egymással?
Megoldás (DOC),
Megoldás (PDF)
T. 261 Egy 8 résztvevős sakkversenyen mindenki
mindenkivel játszik. Döntetlen esetén (és csakis ebben az esetben) váltott
színnel újrajátsszák a partit és a második mérkőzés eredménye kerül a
jegyzőkönyvbe. Előfordulhat-e, hogy a bajnokság során két résztvevő
11-szer, egy 10-szer, három 8-szor és kettő 7-szer
játszott?
Megoldás (DOC),
Megoldás (PDF)
T. 262 Legfeljebb hány színt használhatunk egy 4×4-es
négyzet kifestéséhez (egy-egy rácsnégyzetet egy-egy színnel festünk), ha
azt akarjuk, hogy minden 2×2-es négyzetben legyen két egyforma színű
rácsnégyzet?
Megoldás (DOC),
Megoldás (PDF)
T. 263 Van-e 1996 darab olyan páronként relatív prím
egész szám, amelyek közül bármely néhány (de legalább kettő) összege
összetett szám?
Megoldás (DOC),
Megoldás (PDF)
T. 264 A és
B egy kör (nem diametrálisan
átellenes) rögzített pontjai. E kör minden
XY átmérőjére (
X
¹ A,
Y ¹ B) bejelöljük az
AX és
a
BY egyenesek metszéspontját. Mit alkotnak az így bejelölt pontok?
Megoldás (DOC),
Megoldás (PDF)
T. 265 Egy pozitív törtszámot
rossznak
nevezünk, ha nem állítható elő a
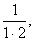
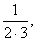
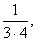 ...
...
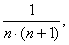 ...
...
sorozat elemei közül véges soknak az
összegeként. Igaz-e, hogy az 1/1996-nál kisebb rossz törtek véges
sokan vannak?
Megoldás (DOC),
Megoldás (PDF)
5. változat
T. 266 Bizonyítsd be, hogy ha 0 <
a <
b <
c <
d, akkor az
x4 +
bx +
c = 0 és az
x4 +
ax +
d = 0 egyenleteknek nincs közös gyöke!
Megoldás (DOC),
Megoldás (PDF)
T. 267 Adott a síkon néhány (de legalább két) pont.
Egy szakaszt, melynek végpontjai az adott pontok közül valók
párosnak (illetve
páratlannak) nevezünk, ha páros (illetve
ha páratlan) sok adott pont van rajta. Bizonyítsd be, hogy több páros
szakasz van, mint páratlan!
Megoldás (DOC),
Megoldás (PDF)
T. 268 Néhány (nem feltétlenül különböző)
pozitív egész szám összege 1996. Lehet-e a reciprokaik összeg éppen 1?
Megoldás (DOC),
Megoldás (PDF)
T. 269 Legfeljebb hány csúcsa lehet egy olyan
sokszögnek, amelynek ha megrajzoljuk mindegyik oldalegyenesét, akkor
összesen csak hat különböző egyenest kapunk a síkon?
Megoldás (DOC),
Megoldás (PDF)
T. 270
Mutasd meg, hogy ha az
x3 +
y3 +
z3 -
3xyz =
n egyenlet megoldható
x, y, z egész
számokkal, akkor az
x3 +
y3 +
z3 -
3xyz = 2
n egyenletnek is van egész
megoldása az
x, y, z változókban.
Megoldás (DOC),
Megoldás (PDF)
T. 271
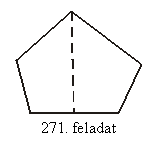
Nevezzük az ötszög súlyvonalának az egyik
csúcsát a szemköztes oldal felezőpontjával összekötő szakaszt! Igaz-e,
hogy az öt súlyvonal minden konvex ötszögben egy közös pontban metszi
egymást?
Megoldás (DOC),
Megoldás (PDF)
T. 272 Osztap Bender egy feketetengeri kaszinó
krupiéjával játszik. A játék során a játékosok felváltva következnek
(először a krupié, utána Osztap), mindig áttéve néhány zsetont a fekete
mezőről a vörösre. Egy lépésben legalább egy, de legfeljebb annyi zsetont
lehet áttenni, amennyi a vörösön már van. Az nyer, aki az utolsó zsetont
teszi át. A játék kezdetén a vörös mezőn 10 zseton volt, a feketén pedig
egy bizonyos mennyiség (de nem nulla), amelyet Osztap jól
megfigyelt. Osztap zsebében még 10 zseton lapul, amelyet a játék
megkezdése előtt szeretne észrevétlenül ráejteni a táblára, néhányat a
fekete, néhányat a vörös mezőre. Bizonyítsd be, hogy ha ügyesen csinálja,
akkor nyerni tud!
Megoldás (DOC),
Megoldás (PDF)
T. 273 Adott a síkon az
A, a
B és a
C pont. Szerkessz olyan
C középpontú kört, amelynek (egyik)
A-t tartalmazó érintője merőleges az (egyik)
B-t tartalmazó
érintőjére!
Megoldás (DOC),
Megoldás (PDF)
6. változat
T. 274 Tíz érménk van melyek tömege rendre 1, 2, 3,
... 10 gramm. Mindegyik érme mellé egy-egy cédulát tettek, amely mutatja
az érme tömegét. Sajnos két, egymástól 1 g-mal eltérő tömegű érme céduláit
felcserélték. Meg lehet-e találni ezt a két érmét egy kétkarú mérleg
kétszeri alkalmazásával, súlyok használata nélkül?
Megoldás (DOC),
Megoldás (PDF)
T. 275 Van-e olyan csupa különböző számjegyből álló
111-gyel osztható pozitív egész szám, amelyben a számjegyek csökkenő
sorrendben következnek egymás után?
Megoldás (DOC),
Megoldás (PDF)
T. 277 Bizonyítsd be, hogy ha egy zárt töröttvonal
bármelyik két oldalának van közös pontja, akkor a töröttvonal páratlan
szakaszból áll!
T. 278 A sakktábla bizonyos mezőin egy-egy bábu áll. A
bábukkal ugorva léphetünk, mindig csak egy szomszédos (függőlegesen,
vízszintesen vagy átlós irányban) mezőn álló bábut ugorhatunk át az
egyenesükön közvetlenül következő mezőre, ha az üres. Legfeljebb hány
bábut lehet úgy elhelyezni a táblán, hogy bármelyikkel megtehessük az első
ugrást?
T. 279 Egy háromszög egyik szöge 30°-os. Bizonyítsd
be, hogy a körülírt kör sugara rövidebb a kerület felénél!
Megoldás (DOC),
Megoldás (PDF)
T. 280 Az "Id Software" cég szörnyeket tenyészt. Ezek
a szörnyek naponta mutálódnak. Ha a szörnynek ma
m keze és
n
lába van, akkor holnap 2
m -
n keze és 2
n -
m
lába lesz. A szörny elpusztul, ha negatív számú keze vagy lába
keletkezik. Bizonyítsd be, hogy akkor és csakis akkor élhet örökké egy
szörny, ha ugyanannyi keze van, mint lába.
Megoldás (DOC),
Megoldás (PDF)
T. 281 A táblán ez olvasható:
ax =
b.
Ketten játszanak.
Kezdő mond egy első számot, majd egy másodikat
is.
Második, saját tetszése szerint, az egyik számot
a-nak,
a másodikat
b-nek felelteti meg. Így egy egyenletet kapnak. Ha a
Kezdő által mondott első szám kielégíti az egyenletet, akkor Kezdő nyer,
egyébként Második a győztes. Kinek van nyerő
stratégiája?
Megoldás (DOC),
Megoldás (PDF)
Írásbeli kiegészítő
forduló
T. 282 Igaz-e, hogy a
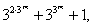
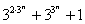
számok bármely m, n különböző pozitív egész számok esetén
relatív prímek egymáshoz?
T. 283 0 Legalább hány lovat kell a sakktáblára tennünk
ahhoz, hogy minden világos mező ütésben álljon?
T. 284 Egy paralelogramma mindegyik oldalán adott egy
pont. El szeretnénk dönteni, hogy a négy pont által meghatározott négyszög
területe megegyezik-e a paralelogramma területének felével. Meg tudjuk-e
mindig válaszolni a kérdést, ha csak egy körző áll a rendelkezésünkre?
Megoldás (DOC),
Megoldás (PDF)
T. 285 Igaz-e, hogy bármely százjegyű pozitív egész
számból kitörölhető az egyik számjegy úgy, hogy a megmaradó szám (jobbról
számított) páros helyein legfeljebb annyi hetes számjegy legyen, mint a
páratlan helyeken?
T. 286 1, 5, 25, 125, ... 5
997 grammos
súlyaink vannak, mindegyikből 2-2, összesen tehát 1996 darab. Meg tudunk-e
mérni ezek és egy kétkarú mérleg segítségével minden olyan egész gramm
tömegű tárgyat, amely nem nehezebb, mint 1996 darab súlyunk összesen?
Megoldás (DOC),
Megoldás (PDF)
T. 287 Egy iskolába 1996 gyerek jár. Mindegyiknek, a
többi 1995 közül pontosan k tetszik. k mely értékei esetén
lehetünk benne biztosak, hogy vagy van két olyan diák, akik tetszenek
egymásnak, vagy van két olyan diák, akik nem tetszenek egymásnak?
Az elődöntő
feladatai
T. 289 Egy kocka minden lapján egy-egy szám látható.
Minden szomszédos lappárnál kiszámoljuk a két lapra írt szám
különbségének abszolút értékét. Bizonyítsd be, hogy az így kapott 12 szám
két hatos csoportba osztható úgy, hogy az egyik csoportban található
számok összege megegyezzen a másik csoportban
találhatókéval!
T. 290 Bizonyítsd be, hogy ha az
ABC és az
OBC háromszög is szabályos és az
M pont az
O
középpontú
OB sugarú körön helyezkedik el, akkor
MA2 =
MB2 +
MC2!
Megoldás (DOC),
Megoldás (PDF)
T. 291 Egy 8×8-as négyzetrács alakú
vonalazást szeretnénk összeállítani kétféle vonaldarab fölhasználásával:
1×1-es négyzet alakú vonalat és olyan derékszöget használhatunk, amelynek
mindkét szára 2 egység. Lehetséges-e ilyen összeállítás, ha a kétféle
építőelemből összesen csak 36-ot használhatunk?
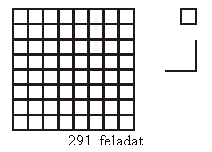
Megoldás (DOC),
Megoldás (PDF)
T. 292 15 csapat olyan bajnokságon méri össze tudását,
amelyben mindegyik csapat mindegyikkel pontosan egyszer játszik.
Bizonyítsd be, hogy a bajnokság során lesz olyan mérkőzés, amelynek két
résztvevője azt megelőzően páratlan mérkőzést játszott!
Megoldás (DOC),
Megoldás (PDF)
T. 293 Peti szétvág egy téglalap alakú papírlapot egy
egyenes mentén. Az így kapott két papírdarab közül az egyiket megint
szétvágja egy egyenes mentén. Ezután a három lap közül választ egyet, és
azt is szétvágja egy egyenes mentén. Így halad tovább. Bizonyítsd be, hogy
kellően sok vágás után a sokszögalakú papírlapok között biztosan lesz 100
darab ugyanannyi oldalú, azaz 100 háromszög, vagy 100 négyszög, stb!
T. 294 Rajzold meg az ABC háromszög CM
súlyvonalát! Az AM és a BC szakaszok
felezőmerőlegeseinek metszéspontja legyen P,
AC és BM felezőmerőlegeseinek metszéspontja pedig Q!
Bizonyítsd be, hogy PQ és CM merőlegesek egymásra!
T. 295 Előfordul-e, hogy M óra N
perckor a nagy és a kis mutató szöge éppen MN ° (M és
N pozitív egész számok)?
A döntő feladatai
T. 296 Az m×n-es négyzetrácsból kivágjuk
a belső mezők által alkotott (m-2)×(n-2)-es részt (m, n
> 2). A megmaradt "szegélyen" ketten játszanak, felváltva lépnek.
Egy lépésben ki lehet vágni bármely - négyzetrácsok alkotta - téglalap
alakú részt (lehet ez egyetlen rácsnégyzet is), csak arra kell ügyelni,
hogy a "szegély" megmaradó része ne essék két részre. Az nyer, aki
utol-jára lép, azaz elveszi a tábla megmaradt (téglalap alakú) részét
(ehhez már nem is kell vágni). Kinek van nyerő stratégiája, annak aki
kezd, vagy a másiknak?
T. 297 Az ABC háromszög B-nél levő
szögének egyik szögharmadolója a C-nél lévő szög egyik
szögharmadolóját a háromszög magasságpontjában metszi. Bizonyítsd be, hogy
ekkor ugyanezen két szög másik szögharmadolói a körülírt kör
középpontjában metszik egymást!
T. 298 Hét biciklis egymáshoz képest kis
időkülönbséggel indult el A-ból B-be. Egyikük egy kulacs
vizet is vitt magával. Ha az egyikük megelőzött egy másikat, és
valamelyiküknél ott volt a kulacs, akkor az mindig átadta a másiknak.
Legalább hány előzésnek kellett lennie az út során, ha tudjuk, hogy
mindenki ivott közben a kulacsból? (Azok az előzések is számításba
veendők, amelyeknél ott se volt a kulacs!)
T. 299 A "kis" dominókészlet 28 dominólapból áll.
Mindegyik lap egyik felét befestették, amihez legfeljebb hét színt
használtak. Mutassuk meg, hogy ki lehet úgy festeni a dominólapok másik
felét, hogy a készlet elemei hét darab négyes csoportba legyenek
sorolhatók és az azonos csoportba tartozó lapok színezése egyforma legyen!
T. 301 El lehet-e helyezni az 1, 2, 3, ..., 20
számokat egy kocka csúcsain és élein úgy, hogy bármelyik élen álló szám az
él két csúcsán álló szám átlaga legyen?
T. 302 A sakktábla minden mezőjén két szöcske ül. Egy
pillanatban mindegyik szöcske átugrik az egyik (vízszintesen vagy
függőleges irányban) szomszédos mezőre úgy, hogy az addig azonos mezőn
tartózkodó szöcskék különböző mezőre ugranak. Legfeljebb hány olyan mező
lesz, amelyre egy szöcske sem ugrik?
T. 303 Úgy töltöttük ki egy 5×5-ös táblázat 25 mezőjét
25 különböző pozitív egész számmal, hogy az öt sorban az elemek
összege egyenlő lett egymással. Lehetséges-e hogy ugyanekkor az öt
oszlopban az elemek szorzata is egyenlő egymással
![]()
![]()
![]() ...
...
![]() ...
...
![]()
![]()
![]() ...
...
![]() ...
...

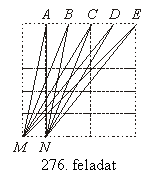 Határozd meg a négyzetrácsra
rajzolt ábrán az MAN, MBN, MCN, MDN és MEN szögek
összegét!
Határozd meg a négyzetrácsra
rajzolt ábrán az MAN, MBN, MCN, MDN és MEN szögek
összegét!![]()
![]()
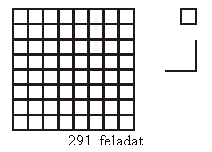
![]()
![]()
![]() ... ,
... ,![]()
![]()